2022-2023學年福建省龍巖市上杭三中、四中、實驗中學八年級（下）期中數學試卷

一、選擇題：每題4分，本題共10小題，共40分。在每小題給出的四個選項中，只有一項是符合要求的。

• 1．要使式子

  x

  -

  3

  有意義，則x的值可以是（　　）

  A．2

  B．0

  C．1

  D．9
  組卷：102引用：5難度：0.7

  解析

• 2．以下列各組數為邊長，可以構成直角三角形的是（　　）

  A．1，1，2

  B．2，3，4

  C．4，5，6

  D．6，8，10
  組卷：22引用：2難度：0.7

  解析

• 3．下列式子是最簡二次根式的是（　　）

  A． 1 2

  B． 8

  C． 2

  D． 0 . 5
  組卷：57引用：1難度：0.8

  解析

• 4．在?ABCD中，∠B=130°，則∠D是（　　）

  A．130°

  B．110°

  C．70°

  D．50°
  組卷：75引用：1難度：0.6

  解析

• 5．已知m=

  4

  +

  3

  ，則以下對m的估算正確的（　　）

  A．2＜m＜3

  B．3＜m＜4

  C．4＜m＜5

  D．5＜m＜6
  組卷：2061引用：13難度：0.9

  解析

• 6．下列命題的逆命題不正確的是（　　）

  A．平行四邊形的兩組對邊相等

  B．矩形的四個角都相等

  C．菱形的四條邊都相等

  D．正方形的對角線互相垂直平分
  組卷：42引用：3難度：0.5

  解析

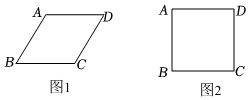• 7．小明用四根長度相同的木條制作了如圖1所示能夠活動的菱形學具，并測得∠B=60°，AC=6cm,接著活動學具成為圖2所示正方形，則圖2中對角線AC的長為（　　）

  A．6cm

  B．3 6 cm

  C．6 2  cm

  D．12 2  cm
  組卷：128引用：5難度：0.7

  解析

• 8．在勾股定理的學習過程中，我們已經學會了運用如圖圖形，驗證著名的勾股定理，這種根據圖形直觀推論或驗證數學規律和公式的方法，簡稱為“無字證明”．實際上它也可用于驗證數與代數，圖形與幾何等領域中的許多數學公式和規律，它體現的數學思想是（　　）
  

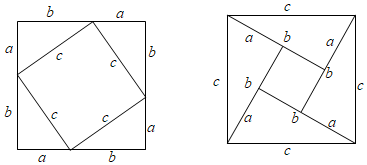
  A．統計思想	B．分類思想
  C．數形結合思想	D．函數思想
  組卷：2653引用：43難度：0.8

  解析

三、解答題：本題共9小題，共86分。解答應寫出文字說明、證明過程或演算步驟。

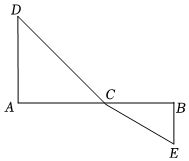• 24．探究：如圖所示，C為線段AB上一動點，分別過點A，點B作AD⊥AB，BE⊥AB，分別連接CD，CE．已知AD=4，BE=2，AB=8．設AC=x.
  （1）CD=

  ，CE=

  （用含x的代數式表示）；
  （2）探究點D，C，E處于何種位置時，CD+CE的值最小，并求出其最小值；
  （3）根據（2）中的探究結果，請構圖并求出代數式

  x

  2

  +

  1

  +

  （

  12

  -

  x

  ）

  2

  +

  16

  的最小值．（要求畫出示意圖）
  組卷：690引用：8難度：0.4

  解析

• 25．如圖1，正方形ABCD中，點O是對角線AC的中點，點P是線段AO上（不與A、O重合）的一個動點，過點P作PE⊥PB且交邊CD于點E．
  （1）求證：PB=PE；
  （2）若正方形ABCD的邊長為6，
  ①過點E作EF⊥AC于點F，如圖2，則在點P運動的過程中，PF的長度是否發生變化？若不變，請直接寫出這個不變的值；若變化，請說明理由．
  ②連接BE交AC于點G，在點P運動的過程中，當CE=2，求PG的長．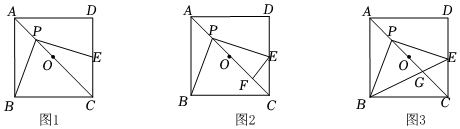
  
  組卷：235引用：2難度：0.2

  解析