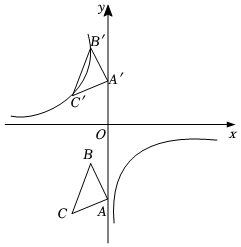
如圖，在平面直角坐標系中，已知△ABC中，AB=AC，∠BAC=90°，已知點A（0，-6）、C（-3，-7），點B在第三象限內．
（1）求點B的坐標；
（2）將△ABC以每秒2個單位的速度沿y軸向上平移t秒，若存在某一時刻t,使在第二象限內點B、C兩點的對應點B'，C'正好落在某反比例函數的圖象上，請求出此時t的值以及這個反比例函數的解析式；
（3）在（2）的情況下，問：是否存在x軸上的點P和反比例函數圖象上的點Q，使得以P、Q、B'、C'四個點為頂點的四邊形是平行四邊形？若存在，請直接寫出符合題意的點Q的坐標；若不存在，請說明理由．
【考點】反比例函數綜合題．
【答案】（1）（-1，-3）；
（2）t=，反比例函數的解析式為：y=-；
（3）存在x軸上的點P和反比例函數圖象上的點Q，使得以P、Q、B'、C'四個點為頂點的四邊形是平行四邊形．Q點坐標為（-，4）或（，-4）或（-，8）．
（2）t=
9
2
6
x
（3）存在x軸上的點P和反比例函數圖象上的點Q，使得以P、Q、B'、C'四個點為頂點的四邊形是平行四邊形．Q點坐標為（-
3
2
3
2
3
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：538引用：1難度：0.3
相似題
-
1．（1）探究新知：
如圖1，已知△ABC與△ABD的面積相等，試判斷AB與CD的位置關系，并說明理由．
（2）結論應用：
①如圖2，點M，N在反比例函數（k＞0）的圖象上，過點M作ME⊥y軸，過點N作NF⊥x軸，垂足分別為E，F．y=kx
試證明：MN∥EF．
發布：2025/6/8 13:0:1組卷：165引用：10難度：0.3 -
2．探究函數性質時，我們經歷了列表、描點、連線畫出函數圖象，觀察分析圖象特征，概括函數性質的過程．結合已有的學習經驗，請畫出函數y=-
的圖象并探究該函數的性質．6x2+1
（1）列表，寫出表中a,b的值：a= ，b= ；x … -4 -3 -2 -1 0 1 2 3 4 … y … - 617- 35- 65-3 -6 a - 65b - 617…
觀察表格中數據的特征，在所給的平面直角坐標系中補全該函數的圖象．
（2）觀察函數圖象，判斷下列關于函數性質的結論是否正確，在括號內打“√”或“×”?
①函數y=-的圖象關于y軸對稱．6x2+1
②當x=0時，函數y=-有最小值，最小值為-6．6x2+1
③在自變量的取值范圍內函數y的值隨自變量x的增大而減小．
④函數y=-的圖象不經過第一、二象限．6x2+1
（3）若將橫、縱坐標都為整數的點稱為整點，直接寫出直線y=a與函數y=-圍成的封閉圖形的內部恰有六個整點時，a的取值范圍．6x2+1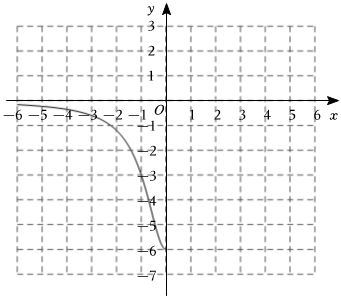
發布：2025/6/6 3:0:2組卷：175引用：2難度：0.4 -
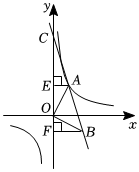3．如圖所示，△OAB的頂點A在反比例函數y=（k＞0）的圖象上，直線AB交y軸于點C，且點C的縱坐標為5，過點A、B分別作y軸的垂線AE、BF，垂足分別為點E、F且AE=1，OE：EC=2：3．kx
（1）求k的值；
（2）若△OAB為等腰直角三角形，∠AOB=90°．求證：△OAE≌△BOF；
（3）把|x1-x2|+|y1-y2|稱為M（x1，y1），N（x2，y2）兩點間的“ZJ距離”，記為d（M，N），在（2）條件下，求d（A，C）+d（A，B）的值．發布：2025/6/8 13:30:1組卷：83引用：1難度：0.1