（2020?棗莊）歐拉（Euler,1707年～1783年）為世界著名的數學家、自然科學家，他在數學、物理、建筑、航海等領域都做出了杰出的貢獻．他對多面體做過研究，發現多面體的頂點數V（Vertex）、棱數E（Edge）、面數F（Flatsurface）之間存在一定的數量關系，給出了著名的歐拉公式．
（1）觀察下列多面體，并把下表補充完整：
| 名稱 | 三棱錐 | 三棱柱 | 正方體 | 正八面體 |
| 圖形 |
|
|
|
|
| 頂點數V | 4 |
6 6
|
8 8
|
6 6
|
| 棱數E | 6 |
9 9
|
12 12
|
12 12
|
| 面數F | 4 |
5 5
|
6 6
|
8 8
|
V+F-E=2
V+F-E=2
；【拓展提問】
（3）一個多面體的面數比頂點數小8，且有30條棱，則這多面體的頂點數是
20
20
；（4）某個玻璃飾品的外形是簡單多面體，它的外表是由三角形和八邊形兩種多邊形拼接而成，且有48個頂點，每個頂點處都有3條棱．設該多面體表面三角形的個數為x個，八邊形的個數為y個，求x+y的值．
【答案】6；8；6；9；12；12；5；6；8；V+F-E=2；20
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：161引用：1難度：0.6
相似題
-
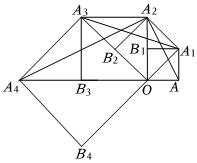1．如圖，四邊形OAA1B1是邊長為1的正方形，以對角線OA1為邊作第二個正方形OA1A2B2，連接AA2，得到△AA1A2；再以對角線OA2為邊作第三個正方形OA2A3B3連接A1A3，得到△A1A2A3；再以對角線OA3為邊作第四個正方形OA3A4B4，連接A2A4，得到△A2A3A4…．設△AA1A2，△A1A2A3，△A2A3A4，…的面積分別為S1，S2，S3，…此下去，則S2023的值為（ ）發布：2025/6/5 2:0:4組卷：47引用：1難度：0.6 -
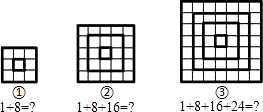2．如圖，觀察圖形及圖形所對應的算式，根據你發現的規律計算1+8+16+24+…+8n（n是正整數）的結果是．發布：2025/6/6 3:0:2組卷：259引用：9難度：0.7 -
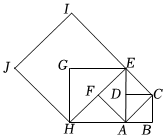3．如圖，四邊形ABCD是邊長為1的正方形，以對角線AC為邊作第二個正方形ACEF，再以對角線AE為邊作第三個正方形AEGH，如此進行下去……記正方形ABCD的邊長為a1=1，按上述方法所作的正方形的邊長依次為a2，a3，a4，……an，則an=．（用含n的式子表示）發布：2025/6/6 3:30:7組卷：25引用：4難度：0.6