綜合與探究
數學活動課上，老師以“一個含45°的直角三角板和兩條平行線”為背景展開探究活動，如圖1，已知直線m∥n,直角三角板ABC中，∠ACB=90°，∠BAC=∠ABC=45°．
（1）如圖1，若∠2=65°，則∠1=20°20°；（直接寫出答案）
（2）“啟航”小組在圖1的基礎上繼續展開探究：如圖2，調整三角板的位置，當三角板ABC的直角頂點C在直線n上，直線m與AB，AC相交時，他們得出的結論是：∠1-∠2=135°，你認為啟航小組的結論是否正確，請說明理由；
（3）如圖3，受到“啟航”小組的啟發，“睿智”小組提出的問題是：在圖2的基礎上，繼續調整三角板的位置，當點C不在直線n上，直線m與AC，BC相交時，∠1與∠2有怎樣的數量關系？請你用平行線的知識說明理由．
【考點】平行線的判定與性質．
【答案】20°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/1 8:0:9組卷：198引用：2難度：0.5
相似題
-
1．如圖，D是AB上一點，E是AC上一點，∠ADE=60°，∠B=60°，∠AED=40°．
（1）DE和BC平行嗎？
（2）∠C是多少度？為什么？發布：2025/1/23 8:0:2組卷：73引用：2難度：0.7 -
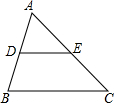2．如圖，D是AB上一點，E是AC上一點，∠ADE=65°，∠B=65°，∠AED=45°．求∠C的度數．發布：2025/1/23 8:0:2組卷：233引用：1難度：0.8 -
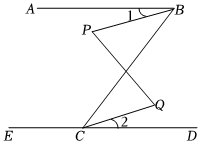3．如圖，∠ABC+∠ECB=180°，∠P=∠Q．
求證：∠1=∠2．
根據圖形和已知條件，請補全下面這道題的解答過程．
證明：∵∠ABC+∠ECB=180° ，
∴AB∥ED ．
∴∠ABC=∠BCD ．
又∵∠P=∠Q（已知），
∴PB∥．
∴∠PBC=．
又∵∠1=∠ABC-，∠2=∠BCD-，
∴∠1=∠2（等量代換）．發布：2024/12/23 20:0:2組卷：1164引用：10難度：0.7