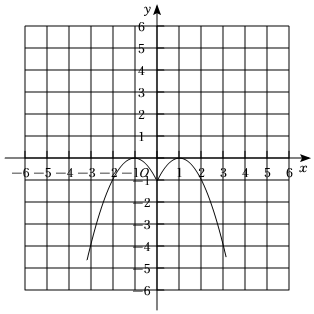
小愛同學學習二次函數后，對函數y=-（|x|-1）2進行了探究．在經歷列表、描點、連線步驟后，得到如圖的函數圖象．請根據函數圖象，回答下列問題：
（1）觀察探究：
①寫出該函數的一條性質：函數圖象關于y軸對稱函數圖象關于y軸對稱；
②方程-（|x|-1）2=-1的解為：x=-2或x=0或x=2x=-2或x=0或x=2；
③若方程-（|x|-1）2=m有四個實數根，則m的取值范圍是 -1＜m＜0-1＜m＜0．
（2）延伸思考：
將函數y=-（|x|-1）2的圖象經過怎樣的平移可得到函數y1=-（|x-1|-1）2+2的圖象？寫出平移過程，并直接寫出當1＜y1≤2時，自變量x的取值范圍．
【答案】函數圖象關于y軸對稱；x=-2或x=0或x=2；-1＜m＜0
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：414引用：4難度：0.6