當前位置：
試題詳情
對于平面直角坐標系xOy中的任意兩點P（x1，y1），Q（x2，y2），給出如下定義：點P與點Q的“直角距離”為：d（P，Q）=|x1-x2|+|y1-y2|．例如：若點M（-1，3），點N（4，1），則點M與點N的“直角距離”為：d（M，N）=|-1-4|+|3-1|=5+2=7．根據以上定義，解決下列問題：
（1）已知點P（4，-3）．
①若點A（2，-4），則d（P，A）=33；
②若點B（b,1），且d（P，B）=6，則b=2或62或6；
③已知點C（m,n）是直線y=-x+2上的一個動點，且d（P，C）＜5，求m的取值范圍．
（2）已知點C（3，0），P為平面直角坐標系內一點，且滿足d（P，C）=2．
①若點P在y=x2-8x+17圖象上，求點P的坐標；
②若點P在直線y=kx+5上，求k的取值范圍．
（3）在平面直角坐標系xOy中，P為動點，且d（O，P）=4，⊙M圓心為M（t,0），半徑為1．若⊙M上存在點N使得PN=1，求t的取值范圍．
【考點】二次函數綜合題．
【答案】3；2或6
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/22 13:30:1組卷：292引用：1難度：0.1
相似題
-
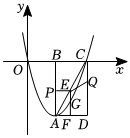1．如圖，在平面直角坐標系中，矩形ABCD的三個頂點B（4，0），C（8，0），D（8，-8），拋物線y=ax2+bx經過A，C兩點，動點P從點A出發，沿線段AB向終點B運動，同時點Q從點C出發，沿線段CD向終點D運動，運動速度均為每秒1個單位長度，運動時間為t秒，過點P作PE⊥AB交AC于點E．
（1）求點A的坐標及拋物線的函數表達式；
（2）過點E作EF⊥AD于點F，交拋物線于點G，當t為何值時，線段EG的長有最大值？最大值是多少？
（3）連接EQ，是否存在t的值使△ECQ為等腰三角形？若存在，請直接寫出t值；若不存在，請說明理由．
（參考公式：平面內兩點P1（x1，y1）、P2（x2，y2）間的距離）（x1-x2）2+（y1-y2）2發布：2025/5/22 17:30:2組卷：201引用：1難度：0.1 -
2．如圖，拋物線y=（x-3）（x-2a）交x軸于A、B兩點（點A在點B的左側），
=OAOB．23
（1）求拋物線的函數表達式；
（2）如圖①，連接BC，點P在拋物線上，且∠BCO=∠PBA．求點P的坐標；12
（3）如圖②，M是拋物線上一點，N為射線CB上的一點，且M、N兩點均在第一象限內，B、N是位于直線AM同側的不同兩點，tan∠AMN=2，點M到x軸的距離為2L，△AMN的面積為5L，且∠ANB=∠MBN，請問MN的長是否為定值？如果是，請求出這個定值；如果不是，請說明理由．
發布：2025/5/22 17:30:2組卷：862引用：8難度：0.3 -
3．已知直線y=3x-3分別與x軸、y軸交于點A，B，拋物線y=ax2+2x+c經過點A，B．
（1）求該拋物線的表達式，并寫出該拋物線的對稱軸和頂點坐標；
（2）記該拋物線的對稱軸為直線l,點B關于直線l的對稱點為C，若點D在y軸的正半軸上，且四邊形ABCD為梯形．
①求點D的坐標；
②將此拋物線向右平移，平移后拋物線的頂點為P，其對稱軸與直線y=3x-3交于點E，若tan∠DPE=，求四邊形BDEP的面積．37發布：2025/5/22 17:30:2組卷：289引用：7難度：0.1