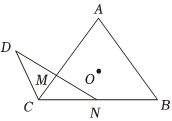
已知△ABC的內角A，B，C的對邊分別為a,b,c,b=c=2，3sinC+cosC=a+bc，點D，P為平面內兩動點，|CD|=1，點N是BC的中點，DN與AC相交于點M（點M異于點A，C），點O為△ABC內切圓圓心，且|PO|=13．
（1）求角A和PA2+PB2+PC2的值；
（2）設CM=tCA（0＜t＜1），g（t）=|NM||ND|，求g（t）的最小值．
3
sin
C
+
cos
C
=
a
+
b
c
|
CD
|
=
1
|
PO
|
=
1
3
PA
2
+
PB
2
+
PC
2
CM
=
t
CA
（
0
＜
t
＜
1
）
g
（
t
）
=
|
NM
|
|
ND
|
【考點】平面向量數量積的性質及其運算．
【答案】（1），的值為；（2）．
A
=
π
3
PA
2
+
PB
2
+
PC
2
13
3
2
3
-
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/29 8:0:10組卷：15引用：3難度：0.5
