2022-2023學年湖南省永州市高一（下）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．若復數z滿足z（1+i）=2i,則z等于（　　）

  A．1+i

  B．-1+i

  C．1-i

  D．-1-i
  組卷：299引用：15難度：0.9

  解析

• 2．若向量

  a

  ，

  b

  滿足

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，

  a

  ?

  b

  =

  1

  ，則

  a

  與

  b

  的夾角為（　　）

  A． π 4

  B． π 3

  C． 2 π 3

  D． 3 π 4
  組卷：63引用：2難度：0.7

  解析

• 3．△ABC的內角A，B，C的對邊分別為a,b,c,若a=2，

  c

  =

  7

  ，

  cos

  B

  =

  7

  4

  ，則b=（　　）

  A． 3

  B．2

  C． 2 3

  D．4
  組卷：128引用：2難度：0.8

  解析

• 4．袋中有大小質地完全相同的5個球，其中紅球3個，黃球2個，從袋中任意取2個球，則取出的2個球都是紅球的概率為（　　）

  A． 1 10

  B． 2 5

  C． 3 10

  D． 3 5
  組卷：26引用：1難度：0.7

  解析

• 5．在長方體ABCD-A₁B₁C₁D₁中，

  AB

  =

  AD

  =

  2

  3

  ，AA₁=2，則異面直線AD₁與A₁C₁所成角的余弦值為（　　）

  A． 2 4

  B． 3 4

  C． 5 4

  D． 6 4
  組卷：184引用：2難度：0.8

  解析

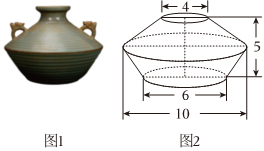• 6．圖1是宋代五大名窯中汝窯制造的雙耳罐，它裝物的有效部分可近似看成由兩個圓臺拼接而成（如圖2所示）在圖2中，已知下底面圓的直徑是6，中間圓的直徑是10，上底面圓的直徑是4，上下底面圓的距離是5，且上、下兩圓臺的高之比是2：3，若不考慮罐壁的厚度，則該汝窯雙耳罐的容積為（　　）

  A．69π

  B．72π

  C．75π

  D．78π
  組卷：29引用：2難度：0.5

  解析

• 7．已知

  OA

  ，

  OB

  ，

  OC

  均為單位向量，

  OA

  +

  2

  OB

  +

  2

  OC

  =

  0

  ，則

  BA

  ?

  BC

  的值為（　　）

  A． 3 8

  B． 5 8

  C． 7 8

  D． 15 8
  組卷：95引用：3難度：0.5

  解析

四、解答題：本題共6小題，共70分解答應寫出文字說明、證明過程或演算步驟．

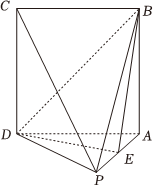• 21．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，正方形ABCD的邊長為2，E是PA的中點．
  （1）求證：PC∥平面BDE；
  （2）若PD=4，線段PC上是否存在一點F，使AF⊥平面BDE？若存在，求出PF的長度；若不存在，請說明理由．（用坐標法解答不給分）
  組卷：259引用：4難度：0.5

  解析

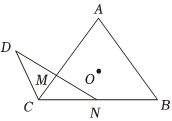• 22．已知△ABC的內角A，B，C的對邊分別為a,b,c,b=c=2，

  3

  sin

  C

  +

  cos

  C

  =

  a

  +

  b

  c

  ，點D，P為平面內兩動點，

  |

  CD

  |

  =

  1

  ，點N是BC的中點，DN與AC相交于點M（點M異于點A，C），點O為△ABC內切圓圓心，且

  |

  PO

  |

  =

  1

  3

  ．
  （1）求角A和

  PA

  2

  +

  PB

  2

  +

  PC

  2

  的值；
  （2）設

  CM

  =

  t

  CA

  （

  0

  ＜

  t

  ＜

  1

  ）

  ，

  g

  （

  t

  ）

  =

  |

  NM

  |

  |

  ND

  |

  ，求g（t）的最小值．
  組卷：15引用：3難度：0.5

  解析