 閱讀理解:在平面直角坐標系中,任意兩點A(x1,y1),B(x2,y2)之間的位置關系有以下三種情形:
閱讀理解:在平面直角坐標系中,任意兩點A(x1,y1),B(x2,y2)之間的位置關系有以下三種情形:
①如果AB∥x軸,則y1=y2,AB=|x1-x2|;
②如果AB∥y軸,則x1=x2,AB=|y1-y2|;
③如果AB與x軸、y軸均不平行,如圖,過點A作與x軸的平行線與過點B作與y軸的平行線相交于點C,則點C坐標為(x2,y1),由①得AC=|x1-x2|,由②得BC=|y1-y2|;根據勾股定理可得平面直角坐標系中任意兩點的距離公式AB=(x1-x2)2+(y1-y2)2.
(1)若點A坐標為(4,6),點B坐標為(1,2),則AB=55;
(2)若點A坐標為(3,3),點B坐標為(6,6),點P是x軸上的動點,直接寫出AP+PB最小值=310310;
(3)已知M=(6-x)2+16+(3-x)2+4,N=(6-x)2+16-(3-x)2+4,根據數形結合,求出M的最小值?N的最大值?
(
x
1
-
x
2
)
2
+
(
y
1
-
y
2
)
2
10
10
(
6
-
x
)
2
+
16
(
3
-
x
)
2
+
4
(
6
-
x
)
2
+
16
(
3
-
x
)
2
+
4
【答案】5;3
10
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:512引用:2難度:0.4
相似題
-
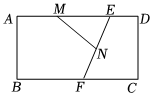 1.如圖,矩形ABCD的邊AB=2,BC=4,E是AD上一點,DE=1,F是BC上一動點,M、N分別是AE、EF的中點,則MN+EN的最小值是 .發布:2025/6/5 23:0:2組卷:432引用:5難度:0.5
1.如圖,矩形ABCD的邊AB=2,BC=4,E是AD上一點,DE=1,F是BC上一動點,M、N分別是AE、EF的中點,則MN+EN的最小值是 .發布:2025/6/5 23:0:2組卷:432引用:5難度:0.5 -
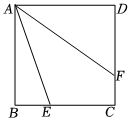 2.如圖,正方形ABCD中,AB=3,動點E、F分別在邊BC、CD上,且保持BE=CF.
2.如圖,正方形ABCD中,AB=3,動點E、F分別在邊BC、CD上,且保持BE=CF.
(1)若BE=CF=1,則AE+AF=;
(2)AE+AF的最小值為 .發布:2025/6/5 23:30:2組卷:101引用:1難度:0.5 -
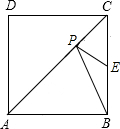 3.如圖,正方形ABCD中,AB=4,E是BC的中點,點P是對角線AC上一動點,則PE+PB的最小值為 .發布:2025/6/6 4:0:1組卷:1273引用:32難度:0.5
3.如圖,正方形ABCD中,AB=4,E是BC的中點,點P是對角線AC上一動點,則PE+PB的最小值為 .發布:2025/6/6 4:0:1組卷:1273引用:32難度:0.5


