我們在分析解決某些數學問題時,經常要比較兩個數或代數的大小,而解決問題的策略一般要進行一定的轉化,其中“作差法”就是常用的方法之一.所謂“作差法”:就是通過作差、變形,并利用差的符號來確定它們的大小,即要比較代數式M、N的大小,只要作出它們的差M-N,若M-N>0,則M>N.若M-N=0,則M=N.若M-N<0,則M<N.請你用“作差法”解決以下問題:
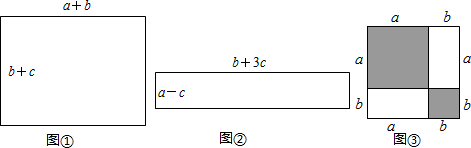
(1)如圖,試比較圖①、圖②兩個矩形的周長C1、C2的大小(b>c);
(2)如圖③,把邊長為a+b(a≠b)的大正方形分割成兩個邊長分別是a、b的小正方形及兩個矩形,試比較兩個小正方形的面積之和S1與兩個矩形面積之和S2的大小.
【考點】整式的混合運算.
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:164引用:1難度:0.3
相似題
-
1.(1)填空:①(-xy2)2=
,②(-x2)3÷(x2)2=,③=(-3x2y)(23xy2),④(2x-1)=2x2-x.
(2)計算:①(x+5y)(2x-y),②(-a)9÷(-a)6?a2+(2a4)2÷a3.發布:2025/6/25 7:30:2組卷:109引用:2難度:0.5 -
2.長方形面積是3a2-3ab+6a,一邊長為3a,則它的周長是
.發布:2025/6/24 19:0:1組卷:145引用:4難度:0.7 -
3.將邊長為m+3的正方形的兩鄰邊長分別增加1和減少1,得到的長方形①的面積為S1.
(1)探究該正方形的面積S與S1的差是否是一個常數,如果是,求出這個常數;如果不是,說明理由;
(2)再將這個正方形兩鄰邊長分別增加4和減少2,得到的長方形②的面積為S2.
①試比較S1,S2的大小;
②當m為正整數時,若某個圖形的面積介于S1,S2之間(不包括S1,S2)且面積為整數,這樣的整數值有且只有14個,求m的值.發布:2025/6/25 8:30:1組卷:22引用:1難度:0.6


