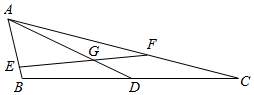
如圖，設△ABC中角A，B，C所對的邊分別為a,b,c,AD為BC邊上的中線，已知c=1且2csinAcosB=asinA-bsinB+
1
4
bsinC，cos∠BAD=
21
7
．
（1）求b邊的長度；
（2）求△ABC的面積；
（3）設點E，F分別為邊AB，AC上的動點，線段EF交AD于G，且△AEF的面積為△ABC面積的一半，求
AG
?
EF
的最小值．

【答案】（1）b=4；（2）△ABC的面積為

；（3）

的最小值是2．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/4/20 14:35:0組卷：1064引用：11難度：0.3

相似題

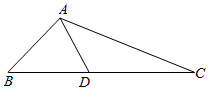1．如圖，在△ABC中，
AB
=
3
6
，
∠
B
=
π
4
，D是BC邊上一點，且
∠
ADB
=
π
3
．
（1）求AD的長；
（2）若CD=10，求AC的長及△ACD的面積．
發布：2025/1/24 8:0:2組卷：324引用：7難度：0.5
解析
2．在華羅庚著的《數學小叢書》中，由一個定理的推導過程，得出一個重要的正弦函數的不等式
sin
α
1
+
sin
α
2
+
…
+
sin
α
n
n
≤sin
α
1
+
α
2
+
…
+
α
n
n
，若四邊形ABCD的四個內角為A，B，C，D，則
sin
A
+
sin
B
+
sin
C
+
sin
D
4
的最大值為（　　）
A．1 B．
3
C．
3
2
D．
2
2
發布：2025/1/5 18:30:5組卷：71引用：1難度：0.7
解析
3．在△ABC中，“A＜B＜C”是“cos2A＞cos2B＞cos2C”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
發布：2025/1/5 18:30:5組卷：190引用：11難度：0.7
解析

相關試卷

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

1．如圖，在△ABC中，AB=36，∠B=π4，D是BC邊上一點，且∠ADB=π3．（1）求AD的長；（2）若CD=10，求AC的長及△ACD的面積．