2022-2023學(xué)年重慶市沙坪壩區(qū)鳳鳴山中學(xué)高一（下）月考數(shù)學(xué)試卷

一、單選題（共8個小題，每小題5分，共40分.）

• 1．若向量

  OB

  =

  （

  3

  ，

  2

  ）

  ，

  AB

  =

  （

  -

  5

  ，

  2

  ）

  ，則點A的坐標為（　　）

  A．（-8，0）

  B．（-2，4）

  C．（2，-4）

  D．（8，0）
  組卷：111引用：3難度：0.8

  解析

• 2．在△ABC中，若∠A=60°，∠B=45°，BC=3

  2

  ，則AC=（　　）

  A． 4 3

  B． 2 3

  C． 3

  D． 3 2
  組卷：2618引用：125難度：0.9

  解析

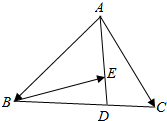• 3．如圖，已知△ABC中，點D在邊BC上，且|BD|=2|DC|，點E在線段AD上，且|AE|=2|ED|，設(shè)

  AB

  =

  a

  ，

  AC

  =

  b

  ，若

  BE

  =m

  a

  +n

  b

  ，則m+n=（　　）

  A．- 1 3

  B． 1 3

  C．-3

  D．3
  組卷：86引用：2難度：0.7

  解析

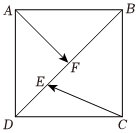• 4．如圖，邊長為2的正方形ABCD中，點E是線段BD上靠近D的三等分點，F(xiàn)是線段BD的中點，則

  AF

  ?

  CE

  =（　　）

  A．-4

  B．-3

  C．-6

  D．-2
  組卷：87引用：1難度：0.8

  解析

• 5．《九章算術(shù)》中，稱底面為矩形而有一側(cè)棱垂直于底面的四棱錐為陽馬，設(shè)AA₁是正六棱柱的一條側(cè)棱，如圖，若陽馬以該正六棱柱的頂點為頂點、以AA₁為底面矩形的一邊，則這樣的陽馬的個數(shù)是（　　）

  A．4

  B．8

  C．12

  D．16
  組卷：3297引用：18難度：0.7

  解析

• 6．已知非零向量

  AB

  與

  AC

  滿足（

  AB

  |

  AB

  |

  +

  AC

  |

  AC

  |

  ）

  ?

  BC

  =0，且

  A

  B

  2

  =

  AB

  ?

  CB

  ，則△ABC為（　　）

  A．等腰非直角三角形	B．直角非等腰三角形
  C．等腰直角三角形	D．等邊三角形
  組卷：301引用：7難度：0.6

  解析

• 7．圣索菲亞大教堂，位于土耳其伊斯坦布爾，有著近一千五百年的歷史，因巨大的圓頂而聞名于世，是一幢拜占庭式建筑．圣索菲亞大教堂主體建筑集中了數(shù)學(xué)的幾何圖形之美，使世界各地的游客前往參觀．現(xiàn)在游客想估算它的高度CD，借助于旁邊高為24米的一幢建筑房屋AB作為參考點，在大教堂與建筑房屋的底部水平線上選取了點P（如圖所示），從點P處測得C點的仰角為60°，測得A點的仰角為45°，從A處測得C處的仰角為30°，則該游客估算圣索菲亞大教堂的高度大約為（　　）
  參考數(shù)據(jù)：

  2

  ≈1.414，

  3

  ≈1.732，

  6

  ≈2.449．

  A．48.68米

  B．53.50米

  C．56.79米

  D．60.24米
  組卷：123引用：4難度：0.7

  解析

四、解答題（共70分，解答應(yīng)寫出必要的文字說明、演算步驟和推理過程.）

• 21．已知向量

  a

  和

  b

  ，

  |

  a

  |

  =

  |

  b

  |

  =

  1

  ，且

  |

  a

  +

  k

  b

  |

  =

  3

  |

  a

  -

  k

  b

  |

  ．
  （1）若

  a

  與

  b

  的夾角為60°，求k的值；
  （2）記

  f

  （

  k

  ）

  =

  a

  ?

  b

  +

  1

  4

  （

  k

  2

  -

  3

  k

  -

  1

  k

  +

  3

  ）

  ，是否存在實數(shù)x,使得f（k）≥1-tx對任意的t∈[-1，1]恒成立？若存在，求出實數(shù)x的取值范圍；若不存在，試說明理由．
  組卷：62引用：2難度：0.5

  解析

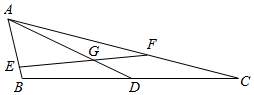• 22．如圖，設(shè)△ABC中角A，B，C所對的邊分別為a,b,c,AD為BC邊上的中線，已知c=1且2csinAcosB=asinA-bsinB+

  1

  4

  bsinC，cos∠BAD=

  21

  7

  ．
  （1）求b邊的長度；
  （2）求△ABC的面積；
  （3）設(shè)點E，F(xiàn)分別為邊AB，AC上的動點，線段EF交AD于G，且△AEF的面積為△ABC面積的一半，求

  AG

  ?

  EF

  的最小值．
  組卷：1064引用：11難度：0.3

  解析