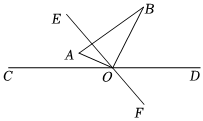
如圖，直線CD與EF相交于點O，∠COE=60°，將一直角三角尺AOB（含30°和60°）的直角頂點與O重合，OA平分∠COE．
（1）求∠BOD的度數；
（2）圖中互余的角有 1212對；
（3）將三角尺AOB以每秒3°的速度繞點O順時針旋轉，同時直線EF以每秒9°的速度繞點O順時針旋轉，設運動時間為t s（0≤t≤40）．
①當t為何值時，直線EF平分∠AOB．
②當t=12s或36s12s或36s時，直線EF平分∠BOD．
【答案】12；12s或36s
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/20 8:0:8組卷：1505引用：5難度：0.3
相似題
-
1．我們將內角互為對頂角的兩個三角形稱為“對頂三角形”．例如，在圖1中，△AOB的內角∠AOB與△COD的內角∠COD互為對頂角，則△AOB與△COD為“對頂三角形”，根據三角形內角和定理知“對頂三角形”有如下性質：∠A+∠B=∠C+∠D．
（1）如圖1，在“對頂三角形”△AOB與△OOD中，∠AOB=70°，則∠C+∠D=°．
（2）如圖2，在△ABC中，AD、BE分別平分∠BAC和∠ABC，若∠C=60°，∠ADE比∠BED大6°，求∠BED的度數．
發布：2025/5/24 11:0:1組卷：826引用：3難度：0.5 -
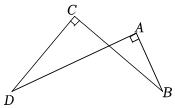2．如圖，∠C=∠A=90°，∠B=25°，則∠D的度數是（ ）發布：2025/5/24 13:30:2組卷：831引用：5難度：0.6 -
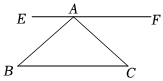3．如圖所示，能利用圖中作法：過點A作BC的平行線，證明三角形內角和是180°的原理是（ ）發布：2025/5/24 10:0:2組卷：112引用：3難度：0.7