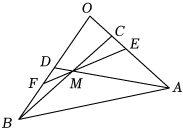
如圖在△AOB中，∠AOB為直角，OC=14OA，OD=12OB，AD與BC相交于點M，OA=a，OB=b．
（1）試用a、b表示向量OM；
（2）在線段AC上取一點E，在線段BD上取一點F，使得直線EF過M，設OE=λOA，OF=μOB，求1λ+3μ的值；
（3）若|AB|=a,過O作線段PQ，使得O為PQ的中點，且|PQ|=2a,求AP?BQ的取值范圍．
OC
=
1
4
OA
，
OD
=
1
2
OB
，
AD
與
BC
相交于點
M
，
OA
=
a
，
OB
=
b
a
、
b
OM
OE
=
λ
OA
，
OF
=
μ
OB
1
λ
+
3
μ
AP
?
BQ
【考點】平面向量數量積的性質及其運算；平面向量的基本定理．
【答案】（1）；（2）7；（3）[-2a2，0]．
1
7
a
+
3
7
b
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：113引用：2難度：0.4
