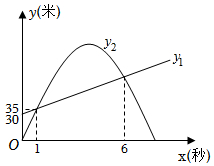
科研人員為了研究彈射器的某項性能，利用無人機測量小鋼球豎直向上運動的相關數據．無人機上升到離地面30米處開始保持勻速豎直上升，此時，在地面用彈射器（高度不計）豎直向上彈射一個小鋼球（忽略空氣阻力），在1秒時，它們距離地面都是35米，在6秒時，它們距離地面的高度也相同．其中無人機離地面高度y1（米）與小鋼球運動時間x（秒）之間的函數關系如圖所示；小鋼球離地面高度y2（米）與它的運動時間x（秒）之間的函數關系如圖中拋物線所示．
（1）直接寫出y1與x之間的函數關系式；
（2）求出y2與x之間的函數關系式；
（3）小鋼球彈射1秒后直至落地時，小鋼球和無人機的高度差最大是多少米？
【考點】二次函數的應用．
【答案】（1）y1與x之間的函數關系式為y1=5x+30；（2）y2與x的函數關系式為y2=-5x2+40x；（3）高度差的最大值為70米．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/4 8:0:9組卷：2940引用：18難度：0.3
相似題
-
1．某超市銷售一種商品，每件成本為50元，銷售人員經調查發現，銷售單價為100元時，每月的銷售量為50件，而銷售單價每降低2元，則每月可多售出10件，且要求銷售單價不得低于成本．
（1）求該商品每月的銷售量y（件）與銷售單價x（元）之間的函數關系式；（不需要求自變量取值范圍）
（2）若使該商品每月的銷售利潤為4000元，并使顧客獲得更多的實惠，銷售單價應定為多少元？
（3）超市的銷售人員發現：當該商品每月銷售量超過某一數量時，會出現所獲利潤反而減小的情況，為了每月所獲利潤最大，該商品銷售單價應定為多少元？發布：2025/6/3 10:0:1組卷：2553引用：17難度：0.6 -
2．為了落實勞動教育，某學校邀請農科院專家指導學生進行小番茄的種植，經過試驗，其平均單株產量y千克與每平方米種植的株數x（2≤x≤8，且x為整數）構成一種函數關系．每平方米種植2株時，平均單株產量為4千克；以同樣的栽培條件，每平方米種植的株數每增加1株，單株產量減少0.5千克．
（1）求y關于x的函數表達式．
（2）每平方米種植多少株時，能獲得最大的產量？最大產量為多少千克？發布：2025/6/3 10:0:1組卷：2294引用：18難度：0.6 -
3．某商店銷售一種銷售成本為每件40元的玩具，若按每件50元銷售，一個月可售出500件．銷售價每漲1元，月銷售量就減少10件．設銷售價為每件x元（x≥50），月銷量為y件，月銷售利潤為w元．
（Ⅰ）當銷售價為每件60元時，月銷量為件，月銷售利潤為元；
（Ⅱ）寫出y與x的函數解析式和w與x的函數解析式；
（Ⅲ）當銷售價定為每件多少元時會獲得最大利潤？求出最大利潤．發布：2025/6/3 10:0:1組卷：969引用：5難度：0.6