 課堂上,老師給出如下命題:
課堂上,老師給出如下命題:
等腰三角形一腰上的高與底邊的夾角等于頂角的一半.
(1)如圖是小明畫出的圖形,請你將已知、求證、證明的過程補充完整.
已知,在△ABC中,AB=AC,BD⊥AC于DAB=AC,BD⊥AC于D.
求證:∠CBD=12∠BAC∠CBD=12∠BAC.
證明:過點A作AE⊥BC于E,
∵AB=AC,
∴∠BAE=∠CAE=12∠BAC,
∵AE⊥BC,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CBD=∠CAE=12∠BAC.過點A作AE⊥BC于E,
∵AB=AC,
∴∠BAE=∠CAE=12∠BAC,
∵AE⊥BC,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CBD=∠CAE=12∠BAC..
(2)利用(1)中的結論解答問題,若等腰三角形的一個內(nèi)角為40度,則該等腰三角形一腰上的高與底邊的夾角為50或2050或20度.
1
2
1
2
∵AB=AC,
∴∠BAE=∠CAE=
1
2
∵AE⊥BC,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CBD=∠CAE=
1
2
∵AB=AC,
∴∠BAE=∠CAE=
1
2
∵AE⊥BC,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CBD=∠CAE=
1
2
【答案】AB=AC,BD⊥AC于D;∠CBD=∠BAC;過點A作AE⊥BC于E,
∵AB=AC,
∴∠BAE=∠CAE=∠BAC,
∵AE⊥BC,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CBD=∠CAE=∠BAC.;50或20
1
2
∵AB=AC,
∴∠BAE=∠CAE=
1
2
∵AE⊥BC,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CBD=∠CAE=
1
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/4/20 14:35:0組卷:342引用:4難度:0.5
相似題
-
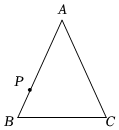 1.如圖,在△ABC中,AB=AC,∠A=50°,P是邊AB上的一個動點,則∠APC的度數(shù)可能是( )
1.如圖,在△ABC中,AB=AC,∠A=50°,P是邊AB上的一個動點,則∠APC的度數(shù)可能是( )A.55° B.62° C.120° D.130° 發(fā)布:2025/5/22 15:0:2組卷:303引用:3難度:0.4 -
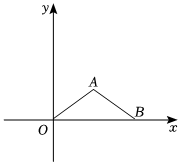 2.如圖,△OAB的頂點O(0,0),點A在第一象限,點B在x軸的正半軸上,若OB=16,OA=AB=10,則點A的坐標是( )
2.如圖,△OAB的頂點O(0,0),點A在第一象限,點B在x軸的正半軸上,若OB=16,OA=AB=10,則點A的坐標是( )A.(10,8) B.(6,8) C.(10,6) D.(8,6) 發(fā)布:2025/5/22 11:30:2組卷:161引用:2難度:0.7 -
3.在△ABC中,BA=BC,在射線BC上取點D,E,且BD<BE,作△ADE,使DA=DE.
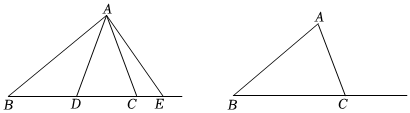
(1)如圖,當點D在線段BC上時,且∠BAD=30°.
①若∠B=40°,求∠EAC的度數(shù);
②若∠B≠40°,求∠EAC的度數(shù);
(2)當點D在BC延長線上時,猜想∠BAD與∠EAC的數(shù)量關系并說明理由.發(fā)布:2025/5/22 16:0:1組卷:689引用:2難度:0.5


