在如圖所示的幾何體中，△ABC是邊長為2的正三角形，AE=1，AE⊥平面ABC，平面BCD⊥平面ABC，BD=CD，且BD⊥CD．
（1）證明：AE∥平面BCD；
（2）證明：平面BDE⊥平面CDE；
（3）求該幾何體的體積．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：226引用：4難度：0.5
相似題
-
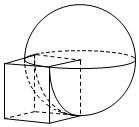1．如圖，將半徑為1的球與棱長為1的正方體組合在一起，使正方體的一個頂點正好是球的球心，則這個組合體的體積為（ ）發布：2024/10/6 12:0:1組卷：479引用：7難度：0.7 -
2．如圖，在矩形ABCD中，E為邊AD的中點，AB=1，BC=2，分別以A、D為圓心，1為半徑作圓弧、?EB（E在線段AD上）．由兩圓弧?EC、?EB及邊BC所圍成的平面圖形繞直線AD旋轉一周，則所形成的幾何體的體積為 ．?EC發布：2024/6/27 10:35:59組卷：343引用：5難度：0.7 -
3．如圖，平面PCBM⊥平面ABC，∠PCB=90°，PM∥BC，直線AM與直線PC所成的角為60°，又AC=1，BC=2PM=2，∠ACB=90°．
（Ⅰ）求證：AC⊥BM；
（Ⅱ）求二面角M-AB-C的大小；
（Ⅲ）求多面體PMABC的體積．發布：2024/6/27 10:35:59組卷：303引用：5難度：0.1