對于“已知x+y=1，求xy的最大值”這個問題，小明是這樣求解的：
∵x+y=1，∴y=1-x,∴xy=x（1-x）=x-x2=-（x-12）2+14；
∴xy≤14，所以xy的最大值為14．
請你按照這種方法計算：當2n+m=4（m＞0，n＞0）時，2m+1n的最小值．
xy
=
x
（
1
-
x
）
=
x
-
x
2
=
-
（
x
-
1
2
）
2
+
1
4
xy
≤
1
4
1
4
2
m
+
1
n
【答案】2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/22 14:0:1組卷：253引用：2難度：0.6
相似題
-
1．二次函數y=3（x-6）2-16的最小值是 ．
發布：2025/5/23 12:30:2組卷：133引用：1難度：0.7 -
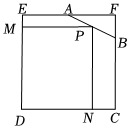2．如圖，已知在邊長為6的正方形FCDE中，A為EF的中點，點B在邊FC上，且BF=2，連接AB，P是線段AB上的一動點，過點P作PM⊥DE，PN⊥DC，垂足分別為M，N，則矩形PNDM面積的最大值是 ．發布：2025/5/23 23:0:1組卷：73引用：1難度：0.5 -
3．如圖Rt△ABC≌Rt△DEF，∠ACB=∠DFE=30°，AB=DE=a,且點B，C，F，E在一條直線上．
（1）沿著EB方向平移△DEF，當F點在線段BC上時，兩個三角形重合部分的面積最大值是 ．
（2）繼續沿直線CF平移△DEF，如圖2，求圖中陰影部分面積的最大值．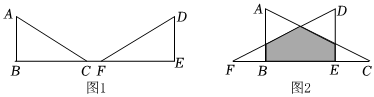
發布：2025/5/24 1:0:1組卷：140引用：1難度：0.5