我們發現平行線具有“等角轉化”的功能，通過添加平行線可將不同位置的角“湊”在一起，得出角之間的關系．根據平行線的“等角轉化”功能，解答下列問題：
（1）閱讀理解：如圖1，AB∥CD，AP，CP相交于點P，請說明∠APC=∠A+∠C．閱讀并補充下面推理過程．
解：過點P作PQ∥AB
∴∠A=∠APQ∠APQ，
∵AB∥CD，
∴PQ∥CDPQ∥CD，
∴∠C=∠CPQ∠CPQ，
∴∠APQ+∠CPQ=∠A+∠C，
即∠APC=∠A+∠C．
（2）方法掌握：如圖2，已知AB∥CD，AM，CM交于點M．請寫出∠A，∠AMC，∠C之間的數量關系，并證明你的結論；
（3）拓展運用：如圖3，已知AB∥CD，點P在直線AB上，CE平分∠PCD，DE平分∠PDC．若∠CPD=n°，求∠CED度數．（用含n的式子表示）
?
【答案】∠APQ；PQ∥CD；∠CPQ
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：418引用：3難度：0.5
相似題
-
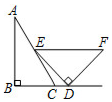1．一副直角三角尺如圖擺放，點D在BC的延長線上，EF∥BC，∠B=∠EDF=90°，∠A=30°，∠F=45°，則∠CED=．發布：2025/5/23 22:0:2組卷：359引用：5難度：0.5 -
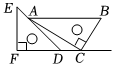2．一副直角三角尺按如圖所示方式放置，點C在FD的延長線上，AB∥FC，∠F=∠ACB=90°，則∠DAC=（ ）發布：2025/5/23 18:0:1組卷：313引用：1難度：0.6 -
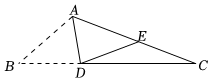3．如圖，將△ABD沿∠BAC的角平分線AD所在直線翻折，點B在AC邊上的落點記為點E，若∠BAC=120°，∠EDC=20°，那么∠C等于（ ）發布：2025/5/23 13:30:1組卷：273引用：4難度：0.7