【問題背景】
小張在預習課本時發現了如下表述:
“關于線段的垂直平分線,有如下的性質定理:線段垂直平分線上的點到線段兩端的距離相等.”小張百思不得其解,對于垂直平分線的性質產生了濃厚的興趣.
【定理證明】
(1)你能幫助小張證明垂直平分線的性質定理嗎?
| 已知:如圖,直線l⊥AB于點O.且OA=OB,C是直線l上的任意一點. 求證:CA=CB |
|

|
證明:①當點C與點O重合時, ∵OA=OB ∴CA=CB ②當點C與點O不重合時, ∵直線l⊥AB ∴∠COA=∠COB=90° 在△COA與△COB中, OA=OB OA=OB ∠AOC=∠BOC ∠AOC=∠BOC CO=CO CO=CO ∴△COA≌△COB( SAS SAS )∴CA=CB |
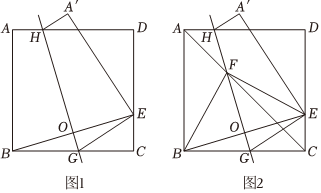
(2)小張在課后折紙活動中驚喜地發現:
如圖1、圖2,將正方形紙片ABCD沿GH折疊.G,H分別在線段BC,AD上,恰好使B點落在線段CD上的點E處,連結BE,交GH于點O,由折疊的性質,直線GH恰為線段BE的垂直平分線.
①如圖1,若正方形紙片的邊長為9cm,AH的長度為2cm,則CG的長度為
4
4
cm.②如圖2,連結對角線AC,與GH交于點F,連結EF,求證:BE=
2
 ?
?【深入探究】
(3)如圖3,在菱形ABCD中,點E為邊CD上的動點,連結BE,AC,作線段BE的垂直平分線分別交AC,BC,BE于點F,G,O,求證:∠BCD=2∠BEF.
【考點】四邊形綜合題.
【答案】OA=OB;∠AOC=∠BOC;CO=CO;SAS;4
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/14 8:0:9組卷:659引用:1難度:0.3
相似題
-
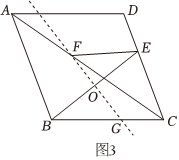
1.如圖,四邊形ABCD是正方形,E是線段BC上一點,連接AE,將AE繞點E順時針旋轉90°,得到EF,過點F作FG⊥CD于點G.
(1)如圖①,當E是BC的中點時,請直接寫出線段FG和BE的數量關系;
(2)如圖②,當E不是BC的中點時,(1)中的結論是否成立?請說明理由;
(3)若BC=4,CE=2,EF與CD交于點P,請求出CP的長.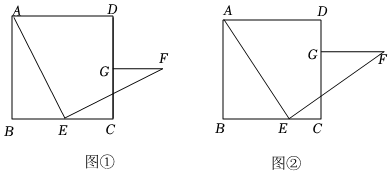 發布:2025/6/20 12:0:2組卷:32引用:1難度:0.1
發布:2025/6/20 12:0:2組卷:32引用:1難度:0.1 -
2.如圖1,正方形ABCD,E為平面內一點,且∠BEC=90°,把△BCE繞點B逆時針旋轉90°得△BAG,直線AG和直線CE交于點F.
(1)證明:四邊形BEFG是正方形;
(2)若∠AGD=135°,猜測CE和CF的數量關系,并說明理由;
(3)如圖2,連接DF,若AB=13,CF=17,求DF的長. 發布:2025/6/20 10:30:1組卷:97引用:1難度:0.1
發布:2025/6/20 10:30:1組卷:97引用:1難度:0.1 -
3.已知:在?ABCD中,∠BAD=45°,AB=BD,E為BC上一點,連接AE交BD于F,過點D作DG⊥AE于G,延長DG交BC于H

(1)如圖1,若點E與點C重合,且AF=,求AD的長;5
(2)如圖2,連接FH,求證:∠AFB=∠HFB;
(3)如圖3,連接AH交BF于M,當M為BF的中點時,請直接寫出AF與FH的數量關系.發布:2025/6/20 10:30:1組卷:532引用:2難度:0.3


