2022-2023學年浙江省寧波市鎮(zhèn)海區(qū)蛟川書院等四校八年級（下）期末數(shù)學試卷

一、選擇題（本題有10小題，每小題4分，共40分。請選出各題中唯一的正確選項）

• 1．下列數(shù)學圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．畢達哥拉斯樹	B．笛卡爾心形線
  C．趙爽弦圖	D．卡西尼卵形線
  組卷：172引用：5難度：0.9

  解析

• 2．下列運算結(jié)果正確的是（　　）

  A． 3 + 2 = 3 2

  B． 32 + 8 = 2 2

  C． 6 × 3 2 = 6 3

  D． 4 1 2 = 2 1 2
  組卷：164引用：1難度：0.8

  解析

• 3．用反證法證明“a＜b“時，首先應(yīng)假設(shè)（　　）

  A．a(chǎn)＜b

  B．a(chǎn)≥b

  C．a(chǎn)≤b

  D．a(chǎn)＞b
  組卷：160引用：2難度：0.9

  解析

• 4．下列方程中：
  ①2x²-1=0．
  ②3（x+2）=-5．
  ③

  1

  x

  2

  -

  2

  =

  1

  ；
  ④

  x

  2

  -

  x

  2

  =5，是一元二次方程的有（　　）

  A．4個

  B．3個

  C．2個

  D．1個
  組卷：461引用：3難度：0.8

  解析

• 5．下列說法不正確的是（　　）

  A．矩形的對角相等，鄰角互補

  B．一組對邊相等且一組對角也相等的四邊形是平行四邊形

  C．一組鄰邊相等的平行四邊形是菱形

  D．對角線互相平分的四邊形是平行四邊形
  組卷：265引用：1難度：0.5

  解析

• 6．一元二次方程2x²-mx+3=0的一根為3，則另一根為（　　）

  A． 1 2

  B．1

  C． 1 3

  D． 3 2
  組卷：464引用：2難度：0.5

  解析

• 7．如圖，在?ABCD內(nèi)部取一點E，連結(jié)AE、BE、CE、DE．若AE=BE=BC 時，恰有∠BAE=30°，則∠DEC的度數(shù)為（　　）

  A．108°

  B．110°

  C．120°

  D．130°
  組卷：124引用：2難度：0.7

  解析

• 8．已知a,b是實數(shù)，定義：aOb=ab+2a-b.若m是常數(shù)，則關(guān)于x的方程：xO（mx）=2，下列說法正確的是（　　）

  A．方程一定有實數(shù)根

  B．當m取某些值時，方程沒有實數(shù)根

  C．方程一定有兩個實數(shù)根

  D．方程一定有兩個不相等的實數(shù)根
  組卷：361引用：1難度：0.7

  解析

三、解答題（本題有8小題，第17-19題每題8分，第20-22題每題10分，第23題14分，第24題12分，

• 23．【問題背景】
  小張在預(yù)習課本時發(fā)現(xiàn)了如下表述：
  “關(guān)于線段的垂直平分線，有如下的性質(zhì)定理：線段垂直平分線上的點到線段兩端的距離相等．”小張百思不得其解，對于垂直平分線的性質(zhì)產(chǎn)生了濃厚的興趣．
  【定理證明】
  （1）你能幫助小張證明垂直平分線的性質(zhì)定理嗎？
  

  已知：如圖，直線l⊥AB于點O．且OA=OB，C是直線l上的任意一點． 求證：CA=CB
  	證明：①當點C與點O重合時， ∵OA=OB ∴CA=CB ②當點C與點O不重合時， ∵直線l⊥AB ∴∠COA=∠COB=90° 在△COA與△COB中， ∴△COA≌△COB（ ） ∴CA=CB

  【定理應(yīng)用】
  （2）小張在課后折紙活動中驚喜地發(fā)現(xiàn)：
  如圖1、圖2，將正方形紙片ABCD沿GH折疊．G，H分別在線段BC，AD上，恰好使B點落在線段CD上的點E處，連結(jié)BE，交GH于點O，由折疊的性質(zhì)，直線GH恰為線段BE的垂直平分線．
  ①如圖1，若正方形紙片的邊長為9cm,AH的長度為2cm,則CG的長度為

  cm.
  ②如圖2，連結(jié)對角線AC，與GH交于點F，連結(jié)EF，求證：BE=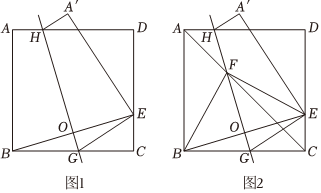

  2

  EF．
  ?
  【深入探究】
  （3）如圖3，在菱形ABCD中，點E為邊CD上的動點，連結(jié)BE，AC，作線段BE的垂直平分線分別交AC，BC，BE于點F，G，O，求證：∠BCD=2∠BEF．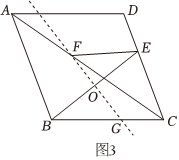
  
  組卷：656引用：1難度：0.3

  解析

• 24．如圖，在菱形ABCD中，∠D=60°，AB=6cm.點P在邊BC上由C向B運動，點Q在邊CD上由D向C運動，速度均為1cm/s,連結(jié)AP、AQ，以AP，AQ為鄰邊構(gòu)造?APMQ，連結(jié)AM過點B作BG⊥AM，交折線A-D-C于點G，分別交AP、AQ于點E、F．
  （1）求證：?APMQ為菱形．
  （2）連結(jié)CE，CF，求△ECF 周長的最小值，并說明理由．
  （3）當點G在線段AD上時，若某時刻滿足DG=DQ，
  ①證明：E為AP中點．
  ②請直接寫出此時P點的運動時間．
  ?
  組卷：561引用：1難度：0.2

  解析