閱讀下列材料：
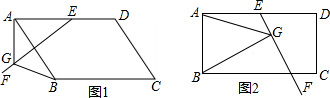
問題：如圖1，在?ABCD中，E是AD上一點，AE=AB，∠EAB=60°，過點E作直線EF，在EF上取一點G，使得∠EGB=∠EAB，連接AG．
求證：EG=AG+BG．
小明同學的思路是：作∠GAH=∠EAB交GE于點H，構造全等三角形，經過推理使問題得到解決．參考小明同學的思路，探究并解決下列問題：
（1）完成上面問題中的證明；
（2）如果將原問題中的“∠EAB=60°”改為“∠EAB=90°”，原問題中的其它條件不變（如圖2），請探究線段EG、AG、BG之間的數量關系，并證明你的結論．
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/6 15:30:1組卷：305引用：3難度：0.1
相似題
-
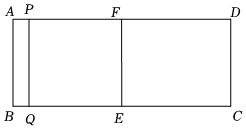1．如圖，在矩形ABCD中，AB=4，BC=10，E、F分別為BC、AD的中點﹒點P從點A出發，以每秒2個單位長度的速度沿AD向終點D勻速運動，作PQ⊥BC于Q，當點P不與點F重合時，設四邊形PQEF的面積為S，點P的運動時間為t（秒）．
（1）當點P與點D重合時，求t的值．
（2）用含t的代數式表示線段PF．
（3）求S與t之間的函數關系式．
（4）當四邊形PQEF的對角線互相垂直時，直接寫出t的值﹒發布：2025/6/7 6:30:1組卷：118引用：2難度：0.4 -
2．如圖1，對角線互相垂直的四邊形叫做垂美四邊形．
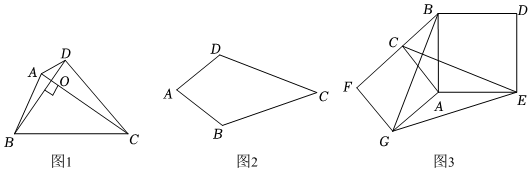
（1）概念理解：如圖2，在四邊形ABCD中，AB=AD，CB=CD，四邊形ABCD是垂美四邊形嗎？請說明理由．
（2）性質探究：如圖1，垂美四邊形ABCD的對角線AC，BD交于點O．AB2，CD2，AD2，BC2的關系是 ．
（3）解決問題：如圖3，分別以Rt△ACB的直角邊AC和斜邊AB為邊向外作正方形ACFG和正方形ABDE，連結CE，BG，GE．已知AC=4，AB=5，求GE的長．（可直接利用（2）中的結論）發布：2025/6/7 6:30:1組卷：322引用：4難度：0.3 -
3．如圖，點M是正方形ABCD的邊BC上一點，連接AM，點E是線段AM上一點，∠CDE的平分線交AM延長線于點F．
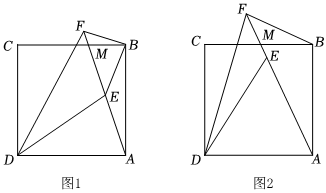
（1）如圖1，若AM=13，BM：CM=5：7，求AB的長；
（2）如圖2，若DA=DE，
①求∠DFA的度數；
②求證：．BF+DF=2AF發布：2025/6/7 6:30:1組卷：75引用：2難度：0.4