定義:我們將能完全覆蓋某平面圖形的圓稱為該平面圖形的覆蓋面.其中,能完全覆蓋平面圖形的最小圓稱為該平面圖形的最小覆蓋圓.
例如:如圖1,線段AB的最小覆蓋圓就是以線段AB為直徑的圓;
[初步思考]
(1)邊長為1cm的正方形的最小覆蓋圓的半徑是 2222cm;
(2)如圖2,邊長為1cm的兩個正方形并列在一起,則其最小覆蓋圓的半徑是 5252cm;
[深入研究]
(1)請分別作出圖3中兩個三角形的最小覆蓋圓(要求用尺規(guī)作圖,保留作圖痕跡,不寫作法).
(2)如圖4,在正方形網格中建立的平面直角坐標系中,△ABC的頂點A位于坐標原點,頂點B、C的坐標分別為(4,0)、(3,3).則△ABC的最小覆蓋圓的圓心坐標為 (2,1)(2,1),半徑長為 55;如圖5,鈍角△MNP中,MN=5,∠MPN=123°,則△MNP的最小覆蓋圓的半徑為 5252.
[生活應用]
某地有四個村莊A,B,C,D(其位置如圖6所示),現(xiàn)擬建一個5G網絡信號中轉站,為了使這四個村莊的居民都能接收到信號,且使中轉站所需發(fā)射功率最小(距離越小,所需功率越小),經過工程人員測量得到CD=8km及圖中相關各角度等數(shù)據(jù),四邊形ABCD區(qū)域最小覆蓋圓的半徑為 833833.
2
2
2
2
5
2
5
2
5
5
5
2
5
2
8
3
3
8
3
3
【考點】圓的綜合題.
【答案】;;(2,1);;;
2
2
5
2
5
5
2
8
3
3
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網所有,未經書面同意,不得復制發(fā)布。
發(fā)布:2024/4/20 14:35:0組卷:219引用:1難度:0.4
相似題
-
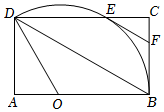 1.如圖,點O是矩形ABCD中AB邊上的一點,以O為圓心,OB為半徑作圓,⊙O交CD邊于點E,且恰好過點D,連接BD,過點E作EF∥BD.
1.如圖,點O是矩形ABCD中AB邊上的一點,以O為圓心,OB為半徑作圓,⊙O交CD邊于點E,且恰好過點D,連接BD,過點E作EF∥BD.
(1)若∠BOD=120°,
①求∠CEF的度數(shù);
②求證:EF是⊙O的切線.
(2)若CF=2,F(xiàn)B=3,求OD的長.發(fā)布:2025/5/25 13:0:1組卷:301引用:3難度:0.4 -
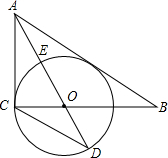 2.如圖,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分線.以O為圓心,OC為半徑作⊙O.
2.如圖,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分線.以O為圓心,OC為半徑作⊙O.
(1)求證:AB是⊙O的切線.
(2)已知AO交⊙O于點E,延長AO交⊙O于點D,tanD=,求12的值.AEAC
(3)在(2)的條件下,設⊙O的半徑為3,求AB的長.發(fā)布:2025/5/25 13:30:1組卷:5031引用:18難度:0.1 -
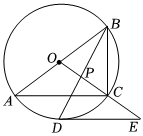 3.如圖,⊙O是△ABC的外接圓,AB是⊙O的直徑、點D為的中點,⊙O的切線DE交OC的延長線于點E.?AC
3.如圖,⊙O是△ABC的外接圓,AB是⊙O的直徑、點D為的中點,⊙O的切線DE交OC的延長線于點E.?AC
(1)求證:DE∥AC;
(2)連接BD交OC于點P,若⊙O的直徑為10、AC=8,求DE的長.發(fā)布:2025/5/25 11:30:2組卷:118引用:1難度:0.5


