2022-2023學年江蘇省鹽城中學南北校區九年級(上)開學數學試卷
發布:2024/4/20 14:35:0
一、選擇題
-
1.下列方程是一元二次方程的是( )
A.3x2-6x+2 B.x2-y+1=0 C.x2=0 D. +x=21x2組卷:357引用:12難度:0.9 -
2.下列采用的調查方式中,不合適的是( )
A.了解澧水河的水質,采用抽樣調查 B.了解一批燈泡的使用壽命,采用全面調查 C.了解張家界市中學生睡眠時間,采用抽樣調查 D.了解某班同學的數學成績,采用全面調查 組卷:1095引用:16難度:0.9 -
3.下列根式中,與
是同類二次根式的是( )3A. 24B. 18C. 20D. 12組卷:200引用:1難度:0.8 -
4.若反比例函數y=
的圖象在第二,四象限,則m的取值范圍是( )2m-1xA.m> 12B.m< 12C.m>2 D.m<2 組卷:1311引用:7難度:0.6 -
5.在公園的O處附近有E、F、G、H四棵樹,位置如圖所示(圖中小正方形的邊長均相等)現計劃修建一座以O為圓心,OA為半徑的圓形水池,要求池中不留樹木,則E、F、G、H四棵樹中需要被移除的為( )
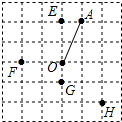
A.E、F、G B.F、G、H C.G、H、E D.H、E、F 組卷:3170引用:19難度:0.7 -
6.為執行國家藥品降價政策,給人民群眾帶來實惠,某藥品經過兩次降價,每瓶零售價由100元降為64元,求平均每次降價的百分率.設平均每次降價的百分率為x,可列方程得( )
A.100(1-x)2=64 B.100(1+x)2=64 C.100(1-2x)=64 D.100(1+2x)=64 組卷:1723引用:25難度:0.7 -
 7.如圖,OA為⊙O的半徑,弦BC⊥OA于點P.若BC=8,AP=2,則⊙O的直徑長為( )
7.如圖,OA為⊙O的半徑,弦BC⊥OA于點P.若BC=8,AP=2,則⊙O的直徑長為( )A.6 B.5 C.10 D.2 17組卷:1197引用:8難度:0.5 -
 8.如圖,四邊形ABCD中,E,F分別是邊AD,BC的中點,G,H分別是對角線BD,AC的中點,若四邊形EGFH為矩形,則四邊形ABCD需滿足的條件是( )
8.如圖,四邊形ABCD中,E,F分別是邊AD,BC的中點,G,H分別是對角線BD,AC的中點,若四邊形EGFH為矩形,則四邊形ABCD需滿足的條件是( )A.AC=BD B.AC⊥BD C.AB=DC D.AB⊥DC 組卷:1409引用:5難度:0.5
二、填空題
-
9.在平行四邊形ABCD中,∠A+∠C=200°,則∠A=.
組卷:663引用:10難度:0.9
三、解答題
-
26.定義:我們將能完全覆蓋某平面圖形的圓稱為該平面圖形的覆蓋面.其中,能完全覆蓋平面圖形的最小圓稱為該平面圖形的最小覆蓋圓.
例如:如圖1,線段AB的最小覆蓋圓就是以線段AB為直徑的圓;
[初步思考]
(1)邊長為1cm的正方形的最小覆蓋圓的半徑是 cm;
(2)如圖2,邊長為1cm的兩個正方形并列在一起,則其最小覆蓋圓的半徑是 cm;
[深入研究]
(1)請分別作出圖3中兩個三角形的最小覆蓋圓(要求用尺規作圖,保留作圖痕跡,不寫作法).
(2)如圖4,在正方形網格中建立的平面直角坐標系中,△ABC的頂點A位于坐標原點,頂點B、C的坐標分別為(4,0)、(3,3).則△ABC的最小覆蓋圓的圓心坐標為 ,半徑長為 ;如圖5,鈍角△MNP中,MN=5,∠MPN=123°,則△MNP的最小覆蓋圓的半徑為 .
[生活應用]
某地有四個村莊A,B,C,D(其位置如圖6所示),現擬建一個5G網絡信號中轉站,為了使這四個村莊的居民都能接收到信號,且使中轉站所需發射功率最小(距離越小,所需功率越小),經過工程人員測量得到CD=8km及圖中相關各角度等數據,四邊形ABCD區域最小覆蓋圓的半徑為 . 組卷:219引用:1難度:0.4
組卷:219引用:1難度:0.4 -
27.如圖,在平面直角坐標系xOy中,已知A(6,0),B(6,4),C(0,4),P為矩形ABCO內一點(不包括邊界),過點P分別作x軸和y軸的平行線,這兩條平行線把矩形ABCO分為四個小矩形,若這四個小矩形中有一個矩形的面積的值等于OA的長度,則稱點P為矩形ABCO的“常積點”.
(1)在點D(4,2.5),E(1,3),F(4,1),G(2,3.5)中,是矩形ABCO“常積點”的為 ;(填寫所有正確的字母代號)
(2)若點H(4m-2,m)是矩形ABCO的“常積點”,且對應的小矩形的一條邊在x軸上,求m的值;
(3)若點M是矩形ABCO的“常積點”,且對應的小矩形的一條邊在x軸上,一次函數y=k(x-5)+7(k為常數,且k>0)的圖象上“常積點”M的個數隨著k的值變化而變化,小明設點M的坐標為(x,y),由(2)解決問題的過程發現符合要求的小矩形有兩類,若是右側的小矩形,可得(6-x)y=6,他發現點M在y=(0<x<66-x)的圖象上,并在原圖形中畫出該函數圖象,請你在小明解決問題的基礎上進一步思考,直接寫出該圖象上“常積點”M的個數及對應的k的取值范圍.92 組卷:165引用:1難度:0.2
組卷:165引用:1難度:0.2


