數學問題:各邊長都是整數,最大邊長為21的三角形有多少個?
為解決上面的數學問題,我們先研究下面的數學模型:
數學模型:在1到21這21個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于21,有多少種不同的取法?
為了找到解決問題的方法,我們把上面數學模型簡單化.
(1)在1~4這4個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于4,有多少種不同的取法?
根據題意,有下列取法:1+4,2+3,2+4,3+2,3+4,4+1,4+2,4+3;而1+4與4+1,2+3與3+2,…是同一種取法,所以上述每一種取法都重復過一次,因此共有1+2+2+32=4=424種不同的取法.
(2)在1~5這5個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于5,有多少種不同的取法?
根據題意,有下列取法: 1+5,2+4,2+5,3+4,3+5,4+2,4+3,4+5; 5+1,5+2,5+3,5+4,而1+5與5+1,2+4與4+2,…是同一種取法,所以上述每一種取法都重復過一次,因此共有1+2+2+3+42=6=52-14種不同的取法.
(3)在1~6這6個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于6,有多少種不同的取法?
根據題意,有下列取法:1+6,2+5,2+6,3+4,3+5,3+6,4+3,4+5,4+6,5+2,5+3,5+4,5+6,6+1,6+2,6+3,6+4,6+5;而1+6與6+1,2+5與5+2,…是同一種取法,所以上述每一種取法都重復過一次,因此共有1+2+3+3+4+52=9=624種不同的取法.
(4)在1~7這7個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于7,有多少種不同的取法?
根據題意,有下列取法:1+7,2+6,2+7,3+5,3+6,3+7,4+5,4+6,4+7,5+3,5+4,5+6,5+7,6+2,6+3,6+4,6+5,6+7,7+1,7+2,7+3,7+4,7+5,7+6;而1+7與7+1,2+6與6+2,…是同一種取法,所以上述每一種取法都重復過一次,因此共有1+2+3+3+4+5+62=12=72-14種不同的取法…
問題解決:
依照上述研究問題的方法,解決上述數學模型和提出的問題
(1)在1~21這21個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于21,有110110種不同的取法;(只填結果)
(2)在1~n(n為偶數)這n個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于n,有n24n24種不同的取法;(只填最簡算式)
(3)在1~n(n為奇數)這n個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于n,有n2-14n2-14種不同的取法;(只填最簡算式)
(4)各邊長都是整數,最大邊長為21的三角形有多少個?(寫出最簡算式和結果,不寫分析過程)
問題拓展:
(5)在1~100這100個自然數中,每次取兩個不同的數,使得所取的兩個數之和大于100,有25002500種不同的取法;(只填結果)
(6)各邊長都是整數,最大邊長為11的三角形有多少個?(寫出最簡算式和結果,不寫分析過程)
(7)各邊長都是整數,最大邊長為31的三角形有多少個?(寫出最簡算式和結果,不寫分析過程)
1
+
2
+
2
+
3
2
4
2
4
1
+
2
+
2
+
3
+
4
2
5
2
-
1
4
1
+
2
+
3
+
3
+
4
+
5
2
6
2
4
1
+
2
+
3
+
3
+
4
+
5
+
6
2
7
2
-
1
4
n
2
4
n
2
4
n
2
-
1
4
n
2
-
1
4
【考點】三角形邊角關系.
【答案】110;;;2500
n
2
4
n
2
-
1
4
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/25 17:30:1組卷:427引用:2難度:0.1
相似題
-
1.在三邊長為自然數、周長不超過100、最長邊與最短邊之差不大于2的三角形中,互不全等的三角形共有
個.發布:2025/5/28 8:30:1組卷:215引用:2難度:0.1 -
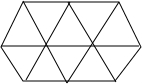 2.對于某些自然數n,可以用n個大小相同的等邊三角形拼成內角都為120°的六邊形.例如,n=10時就可以拼出這樣的六邊形,如圖,請從小到大,求出前10個這樣的n.發布:2025/6/25 8:30:1組卷:39引用:2難度:0.3
2.對于某些自然數n,可以用n個大小相同的等邊三角形拼成內角都為120°的六邊形.例如,n=10時就可以拼出這樣的六邊形,如圖,請從小到大,求出前10個這樣的n.發布:2025/6/25 8:30:1組卷:39引用:2難度:0.3 -
3.三條線段能構成三角形的條件是:任意兩條線段長度的和大于第三條線段的長度.現有長為144cm的鐵絲,要截成n小段(n>2),每段的長度不小于1cm,如果其中任意三小段都不能拼成三角形,則n的最大值為
.發布:2025/5/28 9:0:2組卷:194引用:1難度:0.5


