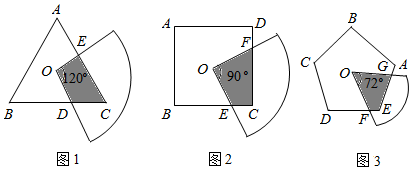
（1）操作：如圖2，O是邊長為a的正方形ABCD的中心，將一塊半徑足夠長、圓心角為直角的扇形紙板的圓心放在O點處，并將紙板繞O點旋轉．求證：正方形ABCD的邊被紙板覆蓋部分的總長度為定值a.
（2）思考：如圖1，將一塊半徑足夠長的扇形紙板的圓心放在邊長為a的正三角形或邊長為a的正五邊形的中心O點處，并將紙板繞O點旋轉．當扇形紙板的圓心角為
120°
120°
時，正三角形的邊被紙板覆蓋部分的總長度為定值a；如圖3，當扇形紙板的圓心角為
72°
72°
時，正五邊形的邊被紙板覆蓋部分的總長度為定值a.（直接填空）
（3）探究：一般地，將一塊半徑足夠長的扇形紙板的圓心放在邊長為a的正n邊形的中心O點處，并將紙板繞O點旋轉，當扇形紙板的圓心角為
360
°
n
360
°
n
度時，正n邊形的邊被紙板覆蓋部分的總長度為定值a；這時正n邊形被紙板覆蓋部分的面積是否也為定值？若為定值，寫出它與正n邊形面積S之間的關系（不需證明）；若不是定值，請說明理由．

【答案】120°；72°；

360

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：204引用：14難度：0.1

相似題

1．如圖，正六邊形ABCDEF內接于圓O，半徑為4，則這個正六邊形的邊心距OM和弧BC的長分別為（　　）
A．2
3
、
4
π
3
B．2
3
、π C．
3
、
2
π
3
D．2、
π
3
發布：2025/5/31 20:0:2組卷：188引用：3難度：0.7
解析
2．如圖，正五邊形ABCDE內接于⊙O，PD與⊙O相切于點D，連接OE并延長，交PD于點P，則∠P的度數是（　　）
A．36° B．28° C．20° D．18°
發布：2025/5/31 22:30:1組卷：1387引用：10難度：0.5
解析
3．如圖，⊙O的半徑為1cm,正六邊形ABCDEF內接于⊙O，則圖中陰影部分面積為
cm²．（結果保留π）
發布：2025/5/31 23:0:1組卷：4173引用：66難度：0.5
解析

相關試卷

1．如圖，正六邊形ABCDEF內接于圓O，半徑為4，則這個正六邊形的邊心距OM和弧BC的長分別為（ ）