2010年新課標八年級數學競賽培訓第29講：圖形的平移與旋轉

一、填空題（共6小題，每小題5分，滿分30分）

• 1．如圖，P為正方形ABCD內一點，PA：PB：PC=1：2：3，則∠APB=

   

  ．
  組卷：541引用：5難度：0.5

  解析

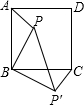• 2．如圖，P是正方形ABCD內一點，將△ABP繞點B順時針方向旋轉能與△CBP′重合，若PB=3，則PP′=

  ．
  組卷：619引用：43難度：0.7

  解析

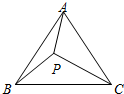• 3．如圖，P是等邊△ABC內一點，PA=6，PB=8，PC=10，則∠APB=

   

  ．
  組卷：227引用：2難度：0.7

  解析

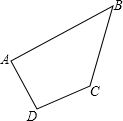• 4．如圖，四邊形ABCD中，AB∥CD，∠D=2∠B，若AD=a,AB=b,則CD的長是

  ．
  組卷：109引用：2難度：0.9

  解析

• 5．在Rt△ABC中，∠A=90°，AB=3cm,AC=4cm,以斜邊BC上距離B點3cm的點P為中心，把這個三角形按逆時針方向旋轉90°到Rt△DEF，則旋轉前后兩個直角三角形重疊部分的面積為

  cm²．
  組卷：758引用：15難度：0.5

  解析

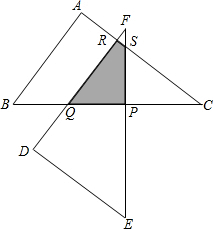
• 6．如圖，在梯形ABCD中，AD∥BC，∠D=90°，BC=CD=12，∠ABE=45°，點E在DC上，AE、BC的延長線交于點F，若AE=10，則S_△ADE+S_△CEF的值是

   

  ．
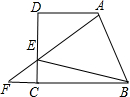  組卷：155引用：3難度：0.5

  解析

二、選擇題（共6小題，每小題3分，滿分18分）

• 7．如圖，在等腰Rt△ABC的斜邊AB上取兩點M，N，使∠MCN=45°，記AM=m,MN=n,BN=x,則以線段x、m、n為邊長的三角形的形狀是（　　）

  A．銳角三角形	B．直角三角形
  C．鈍角三角形	D．隨x、m、n的變化而改變
  組卷：787引用：7難度：0.5

  解析

三、解答題（共11小題，滿分72分）

• 22．如圖，△ABC是等腰三角形，∠C=90°，O是△ABC內一點，點O到△ABC各邊的距離等于1，將△ABC繞點O順時針旋轉45°得到△A₁B₁C₁，兩三角形的公共部分為多邊形KLMNPQ．
  ①證明：△AKL，△BMN，△CPQ都是等腰直角三角形．
  ②求△ABC與△A₁B₁C₁公共部分的面積．
  組卷：42引用：4難度：0.3

  解析

• 23．（1）操作：如圖2，O是邊長為a的正方形ABCD的中心，將一塊半徑足夠長、圓心角為直角的扇形紙板的圓心放在O點處，并將紙板繞O點旋轉．求證：正方形ABCD的邊被紙板覆蓋部分的總長度為定值a.
  （2）思考：如圖1，將一塊半徑足夠長的扇形紙板的圓心放在邊長為a的正三角形或邊長為a的正五邊形的中心O點處，并將紙板繞O點旋轉．當扇形紙板的圓心角為

  時，正三角形的邊被紙板覆蓋部分的總長度為定值a；如圖3，當扇形紙板的圓心角為

  時，正五邊形的邊被紙板覆蓋部分的總長度為定值a.（直接填空）
  （3）探究：一般地，將一塊半徑足夠長的扇形紙板的圓心放在邊長為a的正n邊形的中心O點處，并將紙板繞O點旋轉，當扇形紙板的圓心角為

  度時，正n邊形的邊被紙板覆蓋部分的總長度為定值a；這時正n邊形被紙板覆蓋部分的面積是否也為定值？若為定值，寫出它與正n邊形面積S之間的關系（不需證明）；若不是定值，請說明理由．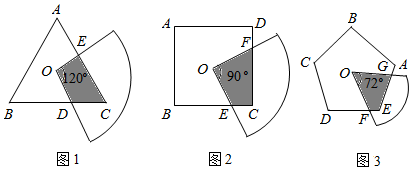
  
  組卷：204引用：14難度：0.1

  解析