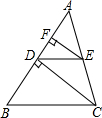
（1）如圖1，CM平分∠ACD，AM平分∠BAC，∠MAC+∠ACM=90°，請判斷AB與CD的位置關系，并證明．
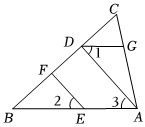
（2）如圖2，∠M=90°，BA∥DC，猜想∠BAM與∠MCD的數量關系并證明．
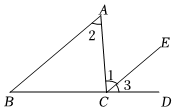
（3）如圖3，G為線段AC上一定點，點H為直線CD上一動點，BA∥DC，當點H在射線CD上運動時（點C上時外）．
①∠BAG+∠AGH+∠DHG=
360
360
°；
②∠CGH，∠CHG與∠BAC有何數量關系？猜想結論并證明．

【答案】360

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：164引用：1難度：0.2

相似題

1．如圖，CD⊥AB于D，EF⊥AB于F．
（1）求證：EF∥CD；
（2）若DE∥BC，EF平分∠AED，求證：CD平分∠ACB．
發布：2025/6/7 19:0:2組卷：974引用：8難度：0.3
解析
2．如圖，已知EF∥AD，∠1=∠2，∠B=40°．
（1）試說明：DG∥AB；
（2）求∠CDG的度數．
發布：2025/6/7 19:0:2組卷：52引用：3難度：0.6
解析
3．如圖，已知點B、C、D在同一直線上，∠B=∠3，∠2=54°，則∠1=（　　）
A．54° B．36° C．48° D．42°
發布：2025/6/7 19:0:2組卷：198引用：2難度：0.7
解析

相關試卷

1．如圖，CD⊥AB于D，EF⊥AB于F．（1）求證：EF∥CD；（2）若DE∥BC，EF平分∠AED，求證：CD平分∠ACB．