在正方形ABCD的對角線AC上任取一點M，連接DM，過點M作DM的垂線交邊AB于點E．
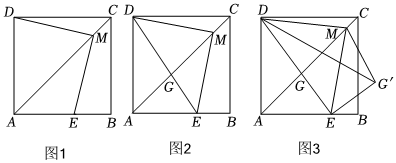
（1）如圖1，寫出DM與ME的數量關系并加以證明；
（2）如圖2，連接DE交AC于點G，若AD=4，AE=3，求DG的長；
（3）在（2）的條件下，將△MGE沿著ME翻折，得到△MG′E，如圖3，連接DG′，求△DMG′的面積．
【考點】四邊形綜合題．
【答案】（1）DM=ME，見解析；
（2）；
（3）．
（2）
DG
=
20
7
（3）
S
△
DMG
′
=
25
7
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：127引用：2難度：0.4
相似題
-
1．在人教版八年級上冊數學教材P53的數學活動中有這樣一段描述：在四邊形ABCD中，AD=CD，AB=CB，我們把這種兩組鄰邊分別相等的四邊形叫做“箏形”，如圖（1）．
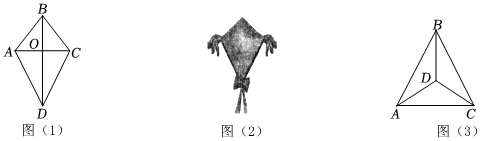
（1）知識應用：小風想要做一個如圖（2）所示的風箏，他想先固定中間的“十字架”，再確定四周，從數學的角度看，小風確定“十字架”時應滿足什么要求？并證明你的結論．
（2）知識拓展：如圖（3）所示，如果D為△ABC內一點，BD平分∠ABC，且AD=CD，試證明：AB=CB．發布：2025/6/9 0:30:2組卷：72引用：1難度：0.2 -
2．矩形ABCD中，∠ACB=30°，△BEF中，∠BEF=90°，∠BFE=30°，BF=
AC，連接FD，點G是FD中點，將△BEF繞點B順時針旋轉α（0°＜α＜360°）．12
（1）如圖1，若點B恰好在線段DF延長線上，AB=4，連接EG，求EG的長度；
（2）如圖2，若點E恰好落在線段FD上，連接AG，證明：2（GD-GA）=DC；3
（3）如圖3，若點E恰好落在線段AB延長線上，點M是線段AD上一點，3AM=DM，N是平面內一點，滿足∠MND=∠FDC，已知AB=4，當△DMN是等腰三角形時，直接寫出線段MN的長度．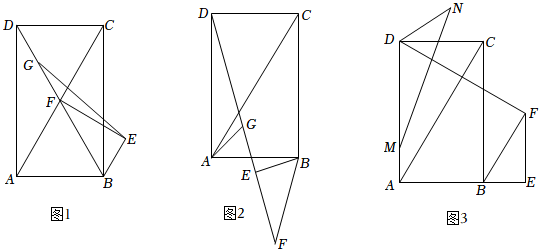
發布：2025/6/9 1:0:1組卷：118引用：1難度：0.1 -
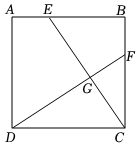3．如圖，正方形ABCD中，AE=BF．
（1）求證：△BCE≌△CDF；
（2）求證：CE⊥DF；
（3）若CD=6，且DG2+GE2=41，則BE=．發布：2025/6/8 23:30:1組卷：360引用：3難度：0.6