綜合與實踐：
數學模型可以用來解決一類問題，是數學應用的基本途徑．通過探究圖形的變化規律，再結合其他數學知識的內在聯系，最終可以獲得寶貴的數學經驗，并將其運用到更廣闊的數學天地．
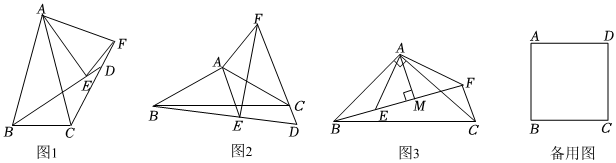
（1）發現問題：如圖1，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=30°，連接BE，CF，延長BE交CF于點D．則BE與CF的數量關系：BE=CFBE=CF，∠BDC=3030°；
（2）類比探究：如圖2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，連接BE，CF，延長BE，FC交于點D．請猜想BE與CF的數量關系及∠BDC的度數，并說明理由；
（3）拓展延伸：如圖3，△ABC和△AEF均為等腰直角三角形，∠BAC=∠EAF=90°，連接BE，CF，且點B，E，F在一條直線上，過點A作AM⊥BF，垂足為點M．則BF，CF，AM之間的數量關系：BF=CF+2AMBF=CF+2AM；
（4）實踐應用：正方形ABCD中，AB=2，若平面內存在點P滿足∠BPD=90°，PD=1，則S△ABP=7+74或7-747+74或7-74．
7
+
7
4
7
-
7
4
7
+
7
4
7
-
7
4
【答案】BE=CF；30；BF=CF+2AM；或
7
+
7
4
7
-
7
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/17 8:0:8組卷：1973引用：6難度：0.5
相似題
-
1．在半徑為1的⊙O中，弦AB、AC的長度分別是
，3，則∠BAC為_____度．（ ）2發布：2025/5/22 15:0:2組卷：189引用：1難度：0.5 -
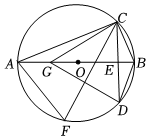2．如圖，在⊙O中，AB為直徑，CD⊥AB于點E，點F為⊙O上一點，點D關于CF的對稱點G恰好在直徑AB上，連接CG，DG，AF，DB．
（1）若∠F=70°，AB=4，則的長為（結果保留π）．?AD
（2）若DB=，AE：BE=5：1，則GE=．6發布：2025/5/22 15:30:1組卷：147引用：2難度：0.4 -
3．如圖，在⊙O中，AB是直徑，CD⊥AB，∠ACD=60°，OD=2，那么DC的長等于（ ）發布：2025/5/22 13:30:1組卷：407引用：7難度：0.7