我們學習等邊三角形時得到特殊直角三角形的一個性質：在直角三角形中，如果一個銳角等于30°，那么它所對的直角邊等于斜邊的一半．即：如圖（1），在Rt△ABC中，∠ACB=90°，∠ABC=30°，則AC=12AB．
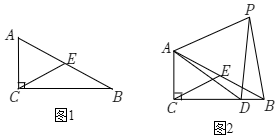
（1）如圖1，作AB邊上的中線CE，得到結論：①△ACE為等邊三角形；②BE與CE之間的數量關系為 BE=CEBE=CE．
（2）如圖2，CE是△ABC的中線，點D是邊CB上任意一點，連接AD，作等邊△ADP，且點P在∠ACB的內部，連接BP．試探究線段BP與DP之間的數量關系，寫出你的猜想并加以證明．
（3）當點D為邊CB延長線上任意一點時，在（2）中條件的基礎上，線段BP與DP之間存在怎樣的數量關系？畫圖并直接寫出答案即可．
AC
=
1
2
AB
【考點】三角形綜合題．
【答案】BE=CE
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：295引用：4難度：0.3
相似題
-
1．有公共頂點C的兩個等腰直角三角形按如圖1所示放置，點E在AB邊上．
（1）連接BD，請直接寫出值為 ；BDAE
（2）如圖2，F，G分別為AB，ED的中點，連接FG，求值；AEFG
（3）如圖3，N為BE的中點，連接CN，AD，求值．ADCN發布：2025/5/21 15:30:1組卷：280引用：1難度：0.3 -
2．【回顧思考】：用數學的思維思考
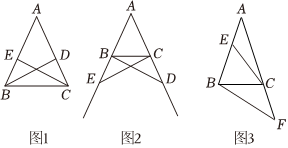
（1）如圖1，在△ABC中，AB=AC．
①若BD，CE是△ABC的角平分線．求證：BD=CE．
②若點D，E分別是邊AC，AB的中點，連接BD，CE．求證：BD=CE．
（從①②兩題中選擇一題加以證明）
（2）【猜想證明】：用數學的眼光觀察
經過做題反思，小明同學認為：在△ABC中，AB=AC，D為邊AC上一動點（不與點A，C重合）對于點D在邊AC上的任意位置，在另一邊AB上總能找到一個與其對應的點E，使得BD=CE．進而提出問題：若點D，E分別運動到邊AC，AB的延長線上，BD與CE還相等嗎？請解決下面的問題：
如圖2，在△ABC中，AB=AC，點D，E分別在邊AC，AB的延長線上，請添加一個條件（不再添加新的字母），使BD=CE，并證明．
（3）【拓展探究】：用數學的語言表達
如圖3，在△ABC中，AB=AC=3，∠A=36°，E為邊AB上任意一點（不與點A，B重合），F為邊AC延長線上一點．判斷BF與CE能否相等．若能，求CF的取值范圍；若不能，說明理由．發布：2025/5/21 17:0:2組卷：305引用：1難度：0.1 -
3．如圖a和圖b,在△ABC中，AB=AC，BC=8，tanC=
．點K在AC邊上，點M，N分別在AB，BC上，且AM=CN=2．點P從點M出發沿折線勻速移動，到達點N時停止；而點Q在AC邊上隨P移動，且始終保持∠APQ=∠B．34
（1）當點P在BC上時，求點P與點A的最短距離：
（2）若點P在MB上，且PO將△ABC的面積分成上下4：5兩部分時，求MP的長；
（3）設點P移動的路程為x,當0≤x≤3及3≤x≤9時，分別求點P到直線AC的距離（用含x的式子表示）；
（4）在點P處設計并安裝一掃描器，按定角∠APQ掃描△APQ區域（含邊界），掃描器隨點P從M到B再到N共用時36秒．若AK=，請直接寫出點K被掃描到的總時長．94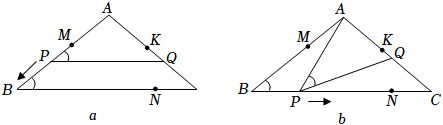
發布：2025/5/21 18:0:1組卷：138引用：1難度：0.2