如圖，正六邊形ABCDEF的邊長(zhǎng)為2，以A為圓心，AC的長(zhǎng)為半徑畫(huà)弧，得
?
EC
，連接AC，AE，則圖中陰影部分的面積為（　　）

A．2π

B．3π

C．

D．

【答案】A

【解答】

【點(diǎn)評(píng)】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。

發(fā)布：2024/7/1 8:0:9組卷：385引用：2難度：0.4

相似題

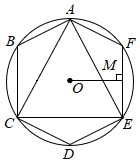1．如圖，已知⊙O的內(nèi)接正六邊形ABCDEF的邊心距OM=1，則該圓的內(nèi)接正三角形ACE的面積為（　　）
A．2 B．4 C．
2
3
D．
3
發(fā)布：2025/5/25 20:30:1組卷：726引用：6難度：0.5
解析
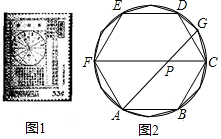2．我國(guó)古代偉大的數(shù)學(xué)家劉徽于公元263年撰《九章算術(shù)注》中指出，“周三徑一”不是圓周率值，實(shí)際上是圓內(nèi)接正六邊形周長(zhǎng)和直徑的比值（圖1）．劉徽發(fā)現(xiàn)，圓內(nèi)接正多邊形邊數(shù)無(wú)限增加時(shí)，多邊形的周長(zhǎng)就無(wú)限逼近圓周長(zhǎng)，從而創(chuàng)立“割圓術(shù)”，為計(jì)算圓周率建立起相當(dāng)嚴(yán)密的理論和完善的算法．如圖2，六邊形ABCDEF是圓內(nèi)接正六邊形，把每段弧二等分，作出一個(gè)圓內(nèi)接正十二邊形，連接AG，CF，AG交CF于點(diǎn)P，若AP=2
6
．則
?
CG
的長(zhǎng)為（　　）
A．
π
2
B．
3
4
π C．
3
3
π D．
2
3
π
發(fā)布：2025/5/25 19:0:2組卷：688引用：8難度：0.4
解析
3．如圖，用若干個(gè)全等的正五邊形排成圓環(huán)狀，圖中所示的是其中3個(gè)正五邊形的位置．要完成這一圓環(huán)排列，共需要正五邊形的個(gè)數(shù)是（　　）
A．7個(gè) B．8個(gè) C．9個(gè) D．10個(gè)
發(fā)布：2025/5/25 17:30:1組卷：993引用：10難度：0.6
解析

相關(guān)試卷

如圖，正六邊形ABCDEF的邊長(zhǎng)為2，以A為圓心，AC的長(zhǎng)為半徑畫(huà)弧，得?EC，連接AC，AE，則圖中陰影部分的面積為（ ）