正方形ABCD的頂點A在直線MN上，點O是對角線AC、BD的交點，過點O作OE⊥MN于點E，過點B作BF⊥MN于點F．
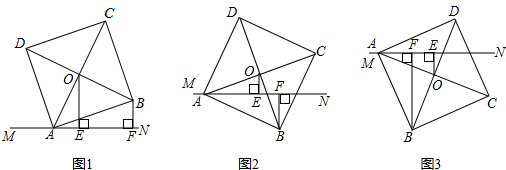
（1）如圖1，當O、B兩點均在直線MN上方時，證明：AF+BF=2OE
（2）當正方形ABCD繞點A順時針旋轉至圖2、圖3的位置時，線段AF、BF、OE之間又有怎樣的關系？請直接寫出你的猜想，并選擇一種情況給予證明．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/6/18 20:30:1組卷：1548引用：62難度：0.3

相似題

1．如圖，在正方形ABCD中，E是對角線AC上一點，AE=AB，則∠EBC=

．
發布：2025/6/19 1:30:1組卷：400引用：10難度：0.7
解析
2．如圖，E是正方形ABCD對角線AC上一點，EF⊥AB，EG⊥BC，F、G是垂足，若正方形ABCD周長為a,則EF+EG等于（　　）
A．
1
4
a
B．
1
2
a
C．a D．2a
發布：2025/6/19 1:0:1組卷：217引用：4難度：0.9
解析
3．矩形、菱形、正方形都是特殊的四邊形，它們具有很多共性，如：
．（填一條即可）
發布：2025/6/19 2:0:1組卷：198引用：18難度：0.9
解析

相關試卷

1．如圖，在正方形ABCD中，E是對角線AC上一點，AE=AB，則∠EBC= ．