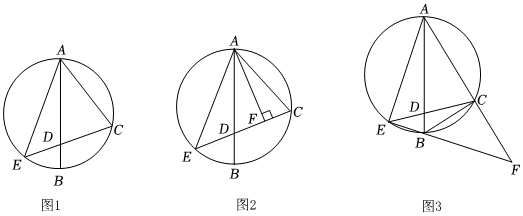
已知點C是以AB為直徑的圓上一點，連結AC，在AB上截取AD=AC，連結CD并延長交圓于點E，連結AE，設AC=kAB．
（1）如圖1，若∠EAB=25°時，求∠BAC度數；
（2）如圖2，過點A作AF⊥CD，證明：CDED=2k；
（3）如圖3，若12＜k＜1，連結EB并延長，交AC的延長線于點F，設△BCF的面積為S1，設△AEF面積為S2，用含k的代數式表示S1：S2．
CD
ED
1
2
【考點】圓的綜合題．
【答案】（1）50°；
（2）證明過程詳見解答；
（2）2-2k．
（2）證明過程詳見解答；
（2）2-2k．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：617引用：2難度：0.1
相似題
-
1．如圖，AB為圓O的直徑，AC為弦，PC為圓O的切線，過點P作PG⊥AB，垂足為G，交AC于點F．
（1）如圖1，求證：PC=PF；
（2）如圖2，連接OF，若OF⊥AC，過點C作CE⊥AB，垂足為E，求證：BE=2OG；
（3）如圖3，在（2）的條件下，延長CE交圓O于點D，連接BF、DF，BF與CE交于點K，若FO平分∠GFB，PG+PC=4，求FD的長．2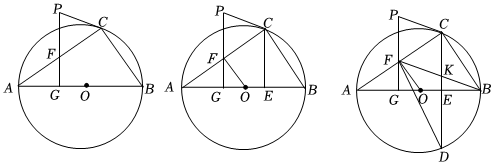
發布：2025/5/22 20:30:1組卷：216引用：1難度：0.2 -
2．【綜合與實踐】我國海域的島嶼資源相當豐富，總面積達72800多平方公里，有人居住的島嶼達450個．位于北部灣的某小島，外形酷似橄欖球，如圖1所示．
如圖2所示，現把海岸線近似看作直線m,小島面對海岸線一側的外緣近似看作AB，經測量，AB的長可近似為250π海里，它所對的圓心角（∠AOB）的大小可近似為90°．（注：AB在m上的正投影為圖中線段CD，點O在m上的正投影落在線段CD上．）
（1）求的半徑r；?AB
（2）因該島四面環海，淡水資源缺乏，為解決島上居民飲用淡水難的問題，擬在海岸線上，建造一個淡水補給站，向島上居民輸送淡水．為節約運輸成本，要求補給站到小島外緣AB的距離最近（即，要求補給站與上的任意一點，兩點之間的距離取得最小值．）；?AB
請你依據所學幾何知識，在圖2中畫出補給站位置及最短運輸路線．（保留畫圖痕跡，并做必要標記與注明；不限于尺規作圖，不要求證明．）
（3）如圖3，若測得AC長為600海里，BD長為500海里，試求出（2）中的最小距離．發布：2025/5/22 20:30:1組卷：763引用：1難度：0.4 -
3．如圖1，在菱形ABCD中，∠DAB=60°，AB=4，以AB為直徑作半圓O交AD于點E，過點E作⊙O的切線交CD于點G，交BA的延長線于點F．當點P從點G運動至點F時，點Q恰好從點A運動至點B，設AQ=x,PF=y.
（1）求證：AF=DG．
（2）求y關于x的函數表達式．
（3）連結PQ．
①當PQ與△AEB的一邊平行時，求x的值．
②如圖2，記PQ與BE交于點M，連結MG，BG．若∠EPM=∠MGB，求△BMQ的面積．發布：2025/5/22 20:0:1組卷：443引用：1難度：0.3