觀察以下等式：
第1個等式：
1
1
+
1
2
×
1
-
1
=2×
1
1
；
第2個等式：
1
2
+
1
2
×
4
-
2
=2×
1
3
；
第3個等式：
1
3
+
1
2
×
9
-
3
=2×
1
5
；
第4個等式：
1
4
+
1
2
×
16
-
4
=2×
1
7
；
第5個等式：
1
5
+
1
2
×
25
-
5
=2×
1
9
；
……
按照以上規律，解決下列問題：
（1）寫出第7個等式：
7-
14
9
=49×
1
9
7-
14
9
=49×
1
9
；
（2）寫出你猜想的第n個等式：
n-
2
n
n
+
2
=n²×
1
n
+
2
n-
2
n
n
+
2
=n²×
1
n
+
2
（用含n的等式表示），并證明．

【答案】7-

=49×

；n-

=n²×

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/6/9 7:30:1組卷：24引用：1難度：0.6

相似題

1．先閱讀理解，再回答下列問題：
因為
1
2
+
1
=
2
，且1＜
2
＜2，所以
1
2
+
1
的整數部分為1；
因為
2
2
+
2
=
6
，且2＜
6
＜3，所以
2
2
+
2
的整數部分為2；
因為
3
2
+
3
=
12
，且3＜
12
＜4，所以
3
2
+
3
的整數部分為3；
（1）以此類推，我們會發現
n
2
+
n
（n為正整數）的整數部分為
；請說明理由；
（2）已知
20
的整數部分為a,
132
的整數部分為b,求a+b的值．
發布：2025/6/9 11:0:1組卷：29引用：1難度：0.6
解析
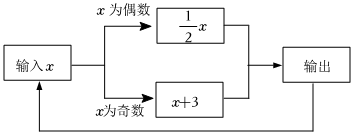
2．如圖所示的運算程序中，若開始輸入的x值為15，則第1次輸出的結果為18，第2次輸出的結果為9，……，第2022次輸出的結果為（　　）
A．3 B．4 C．6 D．9
發布：2025/6/9 5:30:2組卷：428引用：5難度：0.5
解析
3．觀察是數學抽象的基礎，在數學探究學習中，我們要善于通過觀察發現規律，進而解決問題．請你擦亮眼睛，開動腦筋，解答下列問題．
（1）觀察下列等式：
1
1
×
2
=1-
1
2
，
1
2
×
3
=
1
2
-
1
3
，
1
3
×
4
=
1
3
-
1
4
，…
根據發現的規律：
①寫出第5個等式是
，第n個等式是
；
②計算：1×
1
2
+
1
2
×
1
3
+
1
3
×
1
4
+…+
1
2021
×
1
2022
；
（2）思考運用以上方法計算：
1
4
+
1
12
+
1
24
+
1
40
+
1
60
+
1
84
+
1
112
+
1
114
+
1
180
的值．
發布：2025/6/9 7:0:1組卷：62引用：1難度：0.6
解析

相關試卷

2．如圖所示的運算程序中，若開始輸入的x值為15，則第1次輸出的結果為18，第2次輸出的結果為9，……，第2022次輸出的結果為（ ）