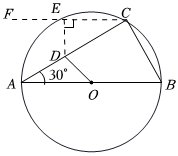
在⊙O中，直徑AB=4，AC是弦，∠CAB=30°，點D是弦AC上的動點，則OD+12CD的最小值是（ ）（為此，我校數學興趣小組的部分同學做了如下探究，如圖，過點C作CF∥AB，過點D作DE⊥CF，得∠ECD=∠CAB=30°，從而DE=12CD，…順著同學們的思路請你做出正確的選擇）
1
2
1
2
【答案】A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/11 14:30:2組卷：115引用：2難度：0.5
相似題
-
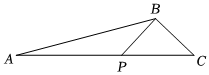1．如圖，在△ACB中，∠A=15°，AB=2，P為AC邊上的一個動點（不與A、C重合），連接BP，則AP+PB的最小值是（ ）22發布：2025/6/5 7:0:2組卷：650引用：4難度：0.4 -
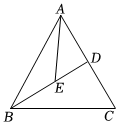2．如圖，△ABC為等邊三角形，BD平分∠ABC，AB=2，點E為BD上動點，連接AE，則的最小值為（ ）AE+12BE發布：2025/6/9 15:0:1組卷：2161引用：3難度：0.6 -
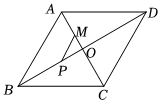3．如圖，在菱形ABCD中，AB=AC=10，對角線AC、BD相交于點O，點M在線段AC上，且AM=4，點P為線段BD上的一個動點，則MP+PB的最小值是（ ）12發布：2025/6/8 12:30:1組卷：475引用：3難度：0.4