如圖（1），形如三角板的△ABC中，∠ACB=90°，∠ABC=45°，BC=12cm,形如矩形量角器的半圓O的直徑DE=12cm,矩形DEFG的寬EF=6cm,矩形量角器以2cm/s的速度從左向右運動，在運動過程中，點D、E始終在BC所在的直線上，設運動時間為x（s），矩形量角器和△ABC的重疊部分的面積為S（cm2）．當x=0（s）時，點E與點C重合．
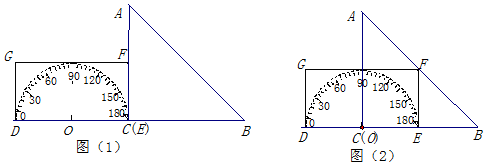
（1）當x=3時，如圖（2），S=3636cm2，當x=6時，S=5454cm2，當x=9時，S=1818cm2；
（2）當3＜x＜6時，求S關于x的函數關系式；
（3）思考：當3＜x＜6時，是否存在某一x的值，使得S=46，并求出此時x的值；
（4）當x為何值時，△ABC的斜邊所在的直線與半圓O所在的圓相切？
【考點】圓的綜合題．
【答案】36；54；18
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/23 13:30:1組卷：19引用：1難度：0.3
相似題
-
1．如圖，在△ACE中，CA=CE，∠CAE=30°，⊙O經過點C，且圓的直徑AB在線段AE上．
（1）試說明CE是⊙O的切線；
（2）若△ACE中AE邊上的高為h,試用含h的代數式表示⊙O的直徑AB；
（3）設點D是線段AC上任意一點（不含端點），連接OD，當CD+OD的最小值為6時，求⊙O的直徑AB的長．12發布：2025/6/23 17:30:1組卷：4522引用：9難度：0.1 -
2．某地質公園為了方便游客，計劃修建一條棧道BC連接兩條進入觀景臺OA的棧道AC和OB，其中AC⊥BC，同時為減少對地質地貌的破壞，設立一個圓形保護區⊙M（如圖所示），M是OA上一點，⊙M與BC相切，觀景臺的兩端A、O到⊙M上任意一點的距離均不小于80米．經測量，OA=60米，OB=170米，tan∠OBC=．43
（1）求棧道BC的長度；
（2）①設OM=x,圓形保護區⊙M的半徑為y,求y關于x的函數關系式，并求出自變量x的取值范圍；
②當點M位于何處時，可以使該圓形保護區的面積最大？發布：2025/6/23 15:0:2組卷：41引用：1難度：0.3 -
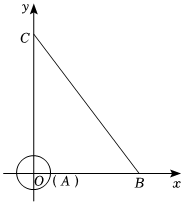3．如圖，在平面直角坐標系中，半徑為1的⊙A的圓心與坐標原點O重合，線段BC的端點分別在x軸與y軸上，點B的坐標為（6，0），且sin∠OCB=．35
（1）若點Q是線段BC上一點，且點Q的橫坐標為m.
①求點Q的縱坐標；（用含m的代數式表示）
②若點P是⊙A上一動點，求PQ的最小值；
（2）若點A從原點O出發，以1個單位/秒的速度沿折線OBC運動，到點C運動停止，⊙A隨著點A的運動而移動．
①點A從O→B的運動的過程中，若⊙A與直線BC相切，求t的值；
②在⊙A整個運動過程中，當⊙A與線段BC有兩個公共點時，直接寫出t滿足的條件．發布：2025/6/23 14:0:1組卷：334引用：5難度：0.1