等差數列{an}中，公差為d,前n項的和為Sn，有如下性質：
（1）通項an=am+（n-m）d；
（2）若m+n=p+q,m、n、p、q∈N*，則am+an=ap+aq；
（3）若m+n=2p,則am+an=2ap；
（4）Sn，S2n-Sn，S3n-S2n構成等差數列．
請類比出等比數列的有關性質．
【考點】類比推理．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：31引用：2難度：0.7
相似題
-
1．已知
tan（x+π4）=1+tanx1-tanx，那么函數y=tanx的周期為π．類比可推出：已知x∈R且（x≠kπ+π4），那么函數y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）發布：2025/1/6 8:0:1組卷：11引用：1難度：0.7 -
2．閱讀下表后，請應用類比的思想，得出橢圓中的結論：
圓 橢圓 定
義平面上到動點P到定點O的距離等于定長的點的軌跡 平面上的動點P到兩定點F1，F2的距離之和等于定值2a的點的軌跡（2a＞|F1F2|） 結
論如圖，AB是圓O的直徑，直線AC，BD是圓O過A，B的切線，P是圓O上任意一點，
CD是過P的切線，則有“PO2=PC?PD”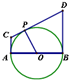
橢圓的長軸為AB，O是橢圓的中心，F1，F2是橢圓的焦點，直線AC，BD是橢圓過A，B的切線，P是橢圓上任意一點，CD是過P的切線，則有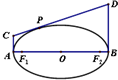 
發布：2025/1/28 8:0:2組卷：32引用：2難度：0.5 -
3．若
，x≠kπ+π4，則y=tanx的周期為π．類比可推出：設x∈R且tan（x+π4）=1+tanx1-tanx，則y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）發布：2025/1/6 8:0:1組卷：36引用：1難度：0.5