 我國魏晉時期的數(shù)學(xué)家劉徽發(fā)現(xiàn)在圓的內(nèi)接正多邊形邊數(shù)加倍的過程中,“割之彌細(xì),所失彌少,割之又割,以至于不可割,則與圓周合體,而無所失矣”,即當(dāng)圓的內(nèi)接正多邊形的邊數(shù)無限增加時,多邊形面積可無限逼近圓面積,他首創(chuàng)了利用圓的內(nèi)接正多邊形確定圓周率.這種確定圓周率的方法稱為( )
我國魏晉時期的數(shù)學(xué)家劉徽發(fā)現(xiàn)在圓的內(nèi)接正多邊形邊數(shù)加倍的過程中,“割之彌細(xì),所失彌少,割之又割,以至于不可割,則與圓周合體,而無所失矣”,即當(dāng)圓的內(nèi)接正多邊形的邊數(shù)無限增加時,多邊形面積可無限逼近圓面積,他首創(chuàng)了利用圓的內(nèi)接正多邊形確定圓周率.這種確定圓周率的方法稱為( )
【答案】C
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/26 8:0:9組卷:18引用:1難度:0.6
相似題
-
1.2019年版一元硬幣的直徑約為22.25mm,則用它能完全覆蓋住的正方形的邊長最大不能超過( )
A.11.125mm B.22.25mm C. mm8928D. mm8938發(fā)布:2025/5/25 23:0:2組卷:119引用:2難度:0.6 -
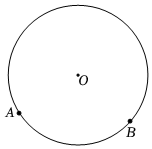 2.如圖,點A,B是半徑為1的圓上的任意兩點,則下列說法正確的是( )
2.如圖,點A,B是半徑為1的圓上的任意兩點,則下列說法正確的是( )A.A,B兩點間的距離可以是 5B.以AB為邊向⊙O內(nèi)構(gòu)造等邊三角形,則三角形的最大面積為 323C.以AB為邊向⊙O內(nèi)構(gòu)造正方形,則正方形的面積可以為3 D.以AB為邊向⊙O內(nèi)構(gòu)造正六邊形,則正六邊形的最大面積為 323發(fā)布:2025/5/26 0:0:1組卷:147引用:2難度:0.4 -
3.半徑為6的圓內(nèi)接正三角形的邊心距為 .
發(fā)布:2025/5/26 0:0:1組卷:202引用:5難度:0.6
相關(guān)試卷


