| 探究遮陽(yáng)傘下的影子長(zhǎng)度 | |||||||
| 素材1 | 圖1是某款自動(dòng)旋轉(zhuǎn)遮陽(yáng)傘，傘面完全張開(kāi)時(shí)張角是180度，圖2是其側(cè)面示意圖．已知支架AB長(zhǎng)為2.5米，且垂直于地面BC，懸托架AE=DE=0.5米，點(diǎn)E固定在傘面上，且傘面直徑DF是DE的4倍．當(dāng)傘面完全張開(kāi)時(shí)，點(diǎn)D，E，F始終共線．為實(shí)現(xiàn)遮陽(yáng)效果最佳，傘面裝有接收器可以根據(jù)太陽(yáng)光線的角度變化，自動(dòng)調(diào)節(jié)手柄D沿著AB上下移動(dòng)，以保證太陽(yáng)光線與DF始終垂直． |
||||||
| 素材2 | 某地區(qū)某天下午不同時(shí)間的太陽(yáng)高度角（太陽(yáng)光線與地面的夾角）參照表： | ||||||
| 時(shí)刻 | 12點(diǎn) | 13點(diǎn) | 14點(diǎn) | 15點(diǎn) | 16點(diǎn) | 17點(diǎn) | |
| 太陽(yáng)高度（度） | 90 | 75 | 60 | 45 | 30 | 15 | |
| 參考數(shù)據(jù)：根號(hào)3≈1.7，根號(hào)2≈1.4 | |||||||
| 素材3 | 小明坐在露營(yíng)椅上的高度（頭頂?shù)降孛娴木嚯x）約為1米，如圖2，小明坐的位置記為點(diǎn)Q | ||||||
| 問(wèn)題解決 | |||||||
| 任務(wù)1 | 確定影子的長(zhǎng)度 | 某一時(shí)刻測(cè)得BD=1.7米，請(qǐng)求出此時(shí)影子GH的長(zhǎng)度． | |||||
| 任務(wù)2 | 判斷是否照射到 | 這天14點(diǎn)，小明坐在離支架3米處的Q點(diǎn)，請(qǐng)判斷此時(shí)小明是否會(huì)被太陽(yáng)光照射到？ 是 是 （填“是”或“否”） |
|||||
| 任務(wù)3 | 探究合理范圍 | 小明打算在這天14：00-15：00露營(yíng)休息，為保證小明全程不被太陽(yáng)光照射到，請(qǐng)直接寫(xiě)出BQ的取值范圍 | |||||
【答案】是
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/30 8:0:9組卷：632引用：1難度：0.5
相似題
-
1．國(guó)際數(shù)學(xué)大會(huì)是全世界數(shù)學(xué)家的大聚會(huì)．如圖是某次大會(huì)的會(huì)徽，選定的是我國(guó)古代數(shù)學(xué)家趙爽用來(lái)證明勾股定理的弦圖，充分肯定了我國(guó)在數(shù)學(xué)方面的成就，也弘揚(yáng)了我國(guó)古代的數(shù)學(xué)文化．如圖，弦圖是由四個(gè)全等的直角三角形和中間的小正方形拼成的一個(gè)大正方形，如果大正方形的面積是25，小正方形的面積是1，直角三角形中較小的銳角為θ，那么cosθ的值等于 ．發(fā)布：2025/5/26 9:30:1組卷：94引用：2難度：0.5 -
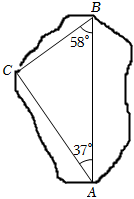2．如圖，湖邊A、B兩點(diǎn)由兩段筆直的觀景棧道AC和CB相連．為了計(jì)算A、B兩點(diǎn)之間的距離，經(jīng)測(cè)量得：∠BAC=37°，∠ABC=58°，AC=80米，求A、B兩點(diǎn)之間的距離．（參考數(shù)據(jù)：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）發(fā)布：2025/5/26 7:30:2組卷：2087引用：10難度：0.5 -
3．如圖，從山下乘纜車上山，纜繩與水平方向成32°的夾角，已知纜車速度為每分鐘50米，從山腳下A到山頂B需16分鐘，則山的高度為（ ）發(fā)布：2025/5/26 7:30:2組卷：612引用：5難度：0.7