【學習概念】有一組對角互余的凸四邊形稱為對余四邊形，連接這兩個角的頂點的線段稱為對余線．
【理解運用】（1）如圖1，對余四邊形中，AB=5，BC=6，CD=4，連接AC，若AC=AB，則cos∠ABC=3535，sin∠CAD=12251225．
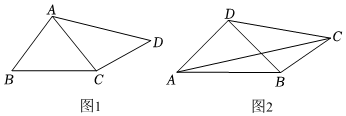
（2）如圖2，凸四邊形中，AD=BD，AD⊥BD，當2CD2+CB2=CA2時，判斷四邊形ABCD是否為對余四邊形，證明你的結(jié)論．
【拓展提升】（3）在平面直角坐標系中，A（-1，0），B（3，0），C（1，2），四邊形ABCD是對余四邊形，點E在對余線BD上，且位于△ABC內(nèi)部，∠AEC=90°+∠ABC．設AEBE=u,點D的縱坐標為t,請在下方橫線上直接寫出u與t的函數(shù)表達，并注明t的取值范圍 u=t2（0＜t＜4）u=t2（0＜t＜4）．
3
5
3
5
12
25
12
25
AE
BE
t
2
t
2
【考點】四邊形綜合題．
【答案】；；u=（0＜t＜4）
3
5
12
25
t
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：883引用：3難度：0.3
相似題
-
1．【基礎鞏固】：
（1）如圖1，在△ABC中，D是BC的中點，E是AC的一個三等分點，且．連結(jié)AD，BE交于點G，則AG：GD=；BG：GE=．AE=13AC
【嘗試應用】：
（2）如圖2，在△ABC中，E為AC上一點，AB=AE，∠BAD=∠C，若AD⊥BE，CE=1，AE=3，求AD的長．
【拓展提高】：
（3）如圖3，在平行四邊形ABCD中，F(xiàn)為BC上一點，E為CD中點，BE與AC，AF分別交于點G，M，若∠BAF=∠DAC，AB=AG，BF=2，BM=2MG，求AM的長．
發(fā)布：2025/5/22 9:0:1組卷：1042引用：5難度：0.3 -
2．定義：我們把對角線相等的凸四邊形叫做“等角線四邊形”．
（1）在已經(jīng)學過的“①平行四邊形；②矩形；③菱形；④正方形“中，一定是“等角線四邊形”的是 （填序號）；
（2）如圖1，在正方形ABCD中，點E，F(xiàn)分別在邊BC，CD上，且EC=DF，連接EF，AF，求證：四邊形ABEF是等角線四邊形；
（3）如圖2，△ABC中，∠ABC=90°，AB=4，BC=3，D為線段AB的垂直平分線上一點，若以點A，B，C，D為頂點的四邊形是等角線四邊形，求這個等角線四邊形的面積．發(fā)布：2025/5/22 9:0:1組卷：478引用：1難度：0.3 -
3．在數(shù)學興趣小組活動中，同學們對矩形的折疊問題進行了探究．在矩形ABCD中，AB=6，AD=3，E是AB邊上一點，AE=2，F(xiàn)是直線CD上一動點，以直線EF為對稱軸，點A關(guān)于直線EF的對稱點為A'．
（1）如圖（1），求四邊形AEA'F的面積．
（2）如圖（2），連接CE，當點A'落在直線CE上時，求tan∠CFA'的值．
（3）當點F，A'，B三點在一條直線上時，則DF的長度為 ．發(fā)布：2025/5/22 9:0:1組卷：225引用：1難度：0.1
相關(guān)試卷