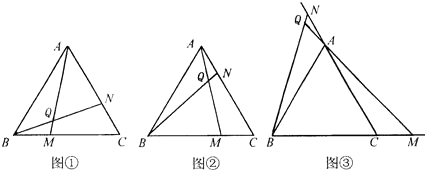
（1）已知△ABC為正三角形，點M是射線BC上任意一點，點N是射線CA上任意一點，且BM=CN，直線BN與AM相交于Q點．就下面給出的三種情況（如圖①、②、③），先用量角器分別測量∠BQM的大小，然后猜測∠BQM等于多少度，并利用圖③證明你的結論．

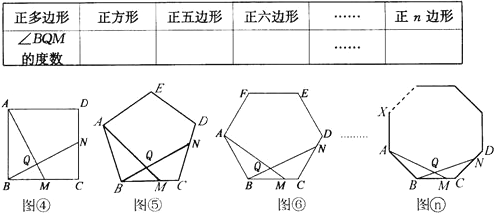
（2）將（1）中的“正△ABC”分別改為正方形ABCD（如圖④）、正五邊形ABCDE（如圖⑤）．正六邊形ABCDEF（如圖③）、…、正n邊形ABCD…X（如圖（n）），“點N是射線CA上任意一點”改為點N是射線CD上任意一點，其余條件不變，根據（1）的求解思路，分別推斷∠BQM各等于多少度，將結論填入下表：

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：318引用：6難度：0.1

相似題

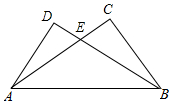1．如圖，∠C=∠D，∠ABC=∠BAD，可證明△ABC≌△BAD．使用了全等三角形的判定定理（　　）
A．SSS B．SAS C．ASA D．AAS
發布：2025/6/1 11:30:2組卷：229引用：3難度：0.7
解析
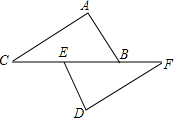2．如圖，點C、E、B、F在同一直線上，CE=BF，AC∥DF，AC=DF，求證：△ABC≌△DEF．
發布：2025/6/1 11:30:2組卷：1702引用：7難度：0.6
解析
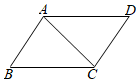3．如圖，AB∥CD，再添加下列條件仍不能判定△ABC≌△CDA的是（　　）
A．BC=AD B．AB=CD C．AD∥BC D．∠B=∠D
發布：2025/6/1 12:0:1組卷：60引用：3難度：0.5
解析

相關試卷

1．如圖，∠C=∠D，∠ABC=∠BAD，可證明△ABC≌△BAD．使用了全等三角形的判定定理（ ）