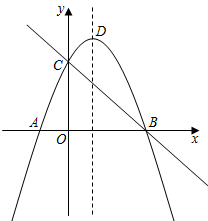
如圖，直線y=-x+3與x軸、y軸分別交于B、C兩點，拋物線y=-x2+bx+c經過點B、C，與x軸另一交點為A，頂點為D．
（1）求拋物線的解析式；
（2）在x軸上找一點E，使EC+ED的值最小，求EC+ED的最小值；
（3）在拋物線的對稱軸上是否存在一點P，使得∠APB=∠OCB？若存在，求出P點坐標；若不存在，請說明理由．
【考點】二次函數綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：879引用：10難度：0.3
相似題
-
1．已知：拋物線y=a（x+3）（x-2）交x軸于點A和點C，與y軸交于點B，且
．tan∠BAC=43
（1）求拋物線解析式；
（2）點P是第四象限拋物線上一點，連接AP交y軸于點F，若點P的橫坐標為t,△ABF的面積為s,求s與t的關系式；
（3）在（2）的條件下，，延長AF、BC交于點G，點H在線段AF上，過點H作HE⊥BC于點E，EH的延長線交拋物線于點D，點M在直線AF下方的第四象限內，連接MH、ME、MG，∠HMG+∠OBC=90°-∠NAC，點N在AG的延長線上，連接MN并延長交x軸于點K，AK=MH，當△MHE的面積為9，點N是MK的中點時，求點D的橫坐標．s=152
?發布：2025/5/22 13:0:1組卷：481引用：3難度：0.1 -
2．如圖，已知二次函數y=-x2+2x+3的圖象交x軸分別于A，D兩點，交y軸于B點，頂點為C．
（1）求拋物線的對稱軸；
（2）求tan∠BAC；
（3）在y軸上是否存在一點P，使得以P，B，D三點為頂點的三角形與△ABC相似？如果存在，請求出點P的坐標；如果不存在，請說明理由．發布：2025/5/22 13:0:1組卷：607引用：7難度：0.3 -
3．定義：如果在給定的自變量取值范圍內，函數既有最大值，又有最小值，則稱該函數在此范圍內有界，函數的最大值與最小值的差叫做該函數在此范圍內的界值．
（1）當-2≤x≤1時，下列函數有界的是 （只要填序號）；
①y=2x-1；②y=-；③y=-x2+2x+3．2x
（2）當m≤x≤m+2時，一次函數y=（k+1）x-2的界值不大于2，求k的取值范圍；
（3）當a≤x≤a+2時，二次函數y=x2+2ax-3的界值為，求a的值．94發布：2025/5/22 13:0:1組卷：1540引用：3難度：0.3