浙教新版九年級上冊《1.4 二次函數的應用》2021年同步練習卷（浙江省金華市婺城區湖海塘中學）
發布：2024/11/11 20:30:2
一．解答題（共22小題）
-
1．如圖，拋物線y=ax2+bx+4交x軸于A（-1，0）、B（3，0）兩點，交y軸于點C，連接BC．
（1）求拋物線的解析式；
（2）點P是拋物線上一點，設P點的橫坐標為m.
①當點P在第一象限時，過點P作PD⊥x軸，交BC于點D，過點D作DE⊥y軸，垂足為E，連接PE，當△PDE和△BOC相似時，求點P的坐標；
②請直接寫出使∠PBA=∠ABC的點P的坐標．12組卷：1054引用：3難度：0.2 -
2．如圖，拋物線y=ax2+2x+c與x軸交于A、B（3，0）兩點，與y軸交于點C（0，3）．
（1）求該拋物線的解析式；
（2）在拋物線的對稱軸上是否存在一點Q，使得以A、C、Q為頂點的三角形為直角三角形？若存在，試求出點Q的坐標；若不存在，請說明理由．組卷：309引用：2難度：0.1 -
3．如圖，已知拋物線過點A（4，0），B（-2，0），C（0，-4）．
（1）求拋物線的解析式；
（2）在圖甲中，點M是拋物線AC段上的一個動點，當圖中陰影部分的面積最小值時，求點M的坐標；
（3）在圖乙中，點C和點C1關于拋物線的對稱軸對稱，點P在拋物線上，且∠PAB=∠CAC1，求點P的橫坐標．
組卷：1285引用：3難度：0.3 -
4．如圖，拋物線y=ax2+bx+c的圖象經過點A（-2，0），點B（4，0），點D（2，4），與y軸交于點C，作直線BC，連接AC、CD．
（1）求拋物線的函數表達式；
（2）E是拋物線上的點，求滿足∠ECD=∠ACO的點E的坐標．
組卷：1651引用：4難度：0.1 -
5．如圖1，拋物線y=ax2+bx+3（a≠0）與x軸、y軸分別交于點A（-1，0）、B（3，0）、點C三點．
（1）試求拋物線的解析式；
（2）點D（2，m）在第一象限的拋物線上，連接BC、BD．試問，在對稱軸左側的拋物線上是否存在一點P，滿足∠PBC=∠DBC？如果存在，請求出點P點的坐標；如果不存在，請說明理由；
（3）如圖2，在（2）的條件下，將△BOC沿x軸正方向以每秒1個單位長度的速度向右平移，記平移后的三角形為△B′O′C′．在平移過程中，△B′O′C′與△BCD重疊的面積記為S，設平移的時間為t秒，試求S與t之間的函數關系式？
組卷：6420引用：13難度：0.1 -
6．如圖，拋物線y=-x2+bx+c與直線y=
x+2交于C、D兩點，其中點C在y軸上，點D的坐標為（3，12）．72
（1）求拋物線的解析式；
（2）點P是y軸右側的拋物線上一個動點，過點P作PE⊥x軸于點E，交直線CD于點F．若點P的橫坐標為m,設線段PF的長度為y,求y與m之間的函數關系式，并直接寫出自變量m的取值范圍；
（3）在（2）的條件下，是否存在點P，使∠PCF=45°？若存在，求出點P的坐標；若不存在，請說明理由．
組卷：653引用：2難度：0.5 -
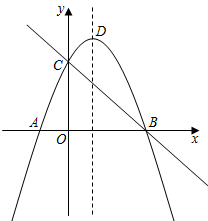7．如圖，直線y=-x+3與x軸、y軸分別交于B、C兩點，拋物線y=-x2+bx+c經過點B、C，與x軸另一交點為A，頂點為D．
（1）求拋物線的解析式；
（2）在x軸上找一點E，使EC+ED的值最小，求EC+ED的最小值；
（3）在拋物線的對稱軸上是否存在一點P，使得∠APB=∠OCB？若存在，求出P點坐標；若不存在，請說明理由．組卷：879引用：10難度：0.3
一．解答題（共22小題）
-
21．如圖所示，在平面直角坐標系中，拋物線y=ax2+bx+c（a≠0）的頂點坐標為C（3，6），并與y軸交于點B（0，3），點A是對稱軸與x軸的交點．
（1）求拋物線的解析式；
（2）如圖①所示，P是拋物線上的一個動點，且位于第一象限，連接BP，AP，求△ABP的面積的最大值；
（3）如圖②所示，在對稱軸AC的右側作∠ACD=30°交拋物線于點D，求出D點的坐標；并探究：在y軸上是否存在點Q，使∠CQD=60°？若存在，求點Q的坐標；若不存在，請說明理由．
組卷：7382引用：40難度：0.4 -
22．綜合與探究
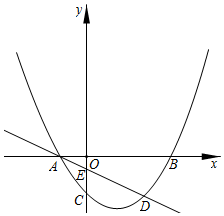
如圖，拋物線y=x2-x-3與x軸交于A，B兩點（點A在點B的左側），與y軸交于點C．直線l與拋物線交于A，D兩點，與y軸交于點E，點D的坐標為（4，-3）．14
（1）請直接寫出A，B兩點的坐標及直線l的函數表達式；
（2）若點P是拋物線上的點，點P的橫坐標為m（m≥0），過點P作PM⊥x軸，垂足為M．PM與直線l交于點N，當點N是線段PM的三等分點時，求點P的坐標；
（3）若點Q是y軸上的點，且∠ADQ=45°，求點Q的坐標．組卷：5018引用：7難度：0.4