如圖1，在矩形ABCD中，AD=4，點(diǎn)O為BC的中點(diǎn)，將△DCO沿DO翻折至△DGO，直線DG分別交直線BC，直線AB于點(diǎn)E，F(xiàn)，連接BG．
（1）試判斷BG與OD的位置關(guān)系，并說明理由．
（2）如圖2，連接AC分別交DE，OD于點(diǎn)H，I，若AC⊥DE，
①求證：OB=2BE．
②求DI的長．
（3）設(shè)直線BG交AD于點(diǎn)K，連接OK，記△ODK的面積為S1，△BOG的面積為S2，連接OF，當(dāng)△DOF中有一個內(nèi)角的正切值為12時，求S1S2的值．
1
2
S
1
S
2
【考點(diǎn)】四邊形綜合題．
【答案】（1）GB∥OD；
（2）①見解答；
②．
（2）①見解答；
②
S
1
S
2
=
5
2
或
5
8
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：406引用：4難度：0.5
相似題
-
1．綜合與實踐課上，老師讓同學(xué)們以“矩形的折疊”為主題開展教學(xué)探究活動．在矩形ABCD中，已知AB=6，BC=8，點(diǎn)P是邊AD上的一個動點(diǎn)．
【操作判斷】
（1）如圖1，甲同學(xué)先將矩形ABCD對折，使得AD與BC重合，展開得到折痕EF．將矩形ABCD沿BP折疊，使A恰好落在EF上的M處，則線段AM與線段PB的位置關(guān)系為 ；∠MBC的度數(shù)為 ；
【遷移探究】
（2）如圖2，乙同學(xué)將矩形ABCD沿BP折疊，使A恰好落在矩形ABCD的對角線上，求此時AP的長；
【綜合應(yīng)用】
（3）如圖3，點(diǎn)Q在邊AB上運(yùn)動，且始終滿足PQ∥BD，以PQ為折疊，將△APQ翻折，求折疊后△APQ與△ABD重疊部分面積的最大值，并求出此時AP的長．
發(fā)布：2025/5/23 0:30:1組卷：594引用：5難度：0.1 -
2．如圖，四邊形ABCD中，AB=BC，∠ABC=120°．連接BD，總有∠DBC=∠DAB+60°．
（1）求∠ADB的度數(shù)；
（2）點(diǎn)F是線段CD的中點(diǎn)，連接BF．
①寫出線段AD，BD，BF之間的數(shù)量關(guān)系，并給出證明；
②延長AD，BF相交于點(diǎn)N，連接CN，若，求線段CN長度的最小值．AB=23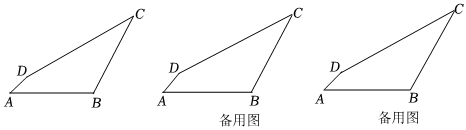
發(fā)布：2025/5/23 1:0:1組卷：457引用：1難度：0.1 -
3．綜合與實踐：情景再現(xiàn)：我們動手操作：把正方形ABCD沿對角線剪開就分剪出兩個等腰直角三角形，把其中一個等腰直角三角形與正方形ABCD重新組合在一起，圖形變得豐富起來，當(dāng)圖形旋轉(zhuǎn)時問題也隨旋轉(zhuǎn)應(yīng)運(yùn)而生．如圖①把正方形ABCD沿對角線剪開，得兩個等腰直角三角形△ACD和△BCE．
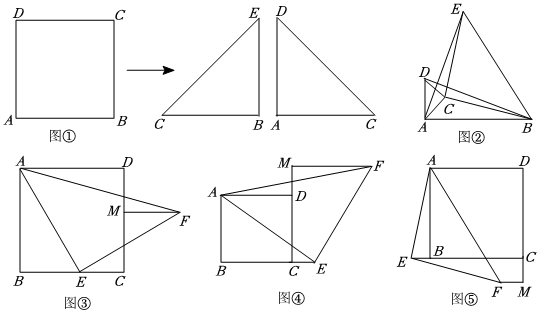
（1）問題呈現(xiàn)，我們把剪下的兩個三角形一個放大另一個縮小拼成如圖②所示的圖形，①若點(diǎn)P是平面內(nèi)一動點(diǎn)，AB=3，PA=1，則線段PB的取值范圍是 ；②直接寫出線段AE與DB的關(guān)系是 ；
（2）我們把剪下的其中一個三角形放大與正方形組合如圖③④⑤所示，點(diǎn)E在直線BC上，F(xiàn)M⊥CD交直線CD于M．①當(dāng)點(diǎn)E在BC上時，如圖③所示，求證：AD=MF+CE；②當(dāng)點(diǎn)E在BC的延長線時，如圖④所示，則線段AD、MF、CE具有的數(shù)量關(guān)系為 ；當(dāng)點(diǎn)E在CB的延長線上時，如圖⑤所示，則線段AD、MF、CE具有的數(shù)量關(guān)系為 ；
（3）在（2）的條件下，連接EM，當(dāng)，其他條件不變，則線段CE的長為 ．S△EMF=8，AF2=50發(fā)布：2025/5/23 1:0:1組卷：158引用：2難度：0.3