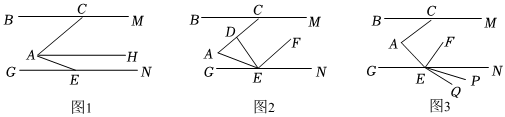
如圖，點E、C分別在直線GN、BM上，點A為平面內BM、CN之間的一點，連接ACAE，若∠CAE=∠BCA+∠AEG．
（1）如圖1，過點A作AH∥BM，試說明：BM∥GN；
（2）如圖2，若∠CAE=60°，AC∥EF，點D在線段AC上，連接DE，且∠FED=2∠BCA，試判斷∠DEA與∠GEA的數量關系，并說明理由；
（3）如圖3，若∠CAE=85°，∠BCA=35°，且EF、EP分別平分∠AEQ、∠NEQ，求∠FEP的度數．
【考點】平行線的判定與性質．
【答案】（1）答案見解答過程；
（2）∠DEA=2∠GEA，理由見解答過程；
（3）65°．
（2）∠DEA=2∠GEA，理由見解答過程；
（3）65°．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/7 8:0:9組卷：211引用：2難度：0.7
相似題
-
1．如圖，AB∥CD∥FH∥GM，且∠EFH=∠GMN．
（1）求證：EG∥HN；
（2）若∠AEG=75°，求∠HNC．發布：2025/6/13 17:0:1組卷：159引用：1難度：0.7 -
2．如圖，CD是△ABC的高，點E、F、G分別在BC、AB、AC上，且EF⊥AB，DG∥BC．試判斷∠1、∠2的數量關系，并說明理由．發布：2025/6/13 13:0:4組卷：390引用：5難度：0.5 -
3．完成下列推理過程：如圖，已知∠A=∠EDF，∠C=∠F，求證：BC∥EF．
證明：∵∠A=∠EDF（已知），
∴∥（ ），
∴∠C=（ ）．
又∵∠C=∠F（已知），
∴=∠F（等量代換），
∴∥（ ）．發布：2025/6/13 18:30:2組卷：234引用：3難度：0.6