計算機是20世紀最偉大的發明之一,被廣泛地應用于工作和生活之中,在進行計算和信息處理時,使用的是二進制.已知一個十進制數n(n∈N*)可以表示成二進制數(a0a1a2…ak)2(k∈N),且n=a0×2k+a1×2k-1+a2×2k-2+…+ak×20,其中a0=1,ai∈{0,1}(i=1,2,3,…,k).記a0,a1,a2,…,ak中1的個數為f(n),若k=9,則滿足f(n)=6的n的個數為( )
【考點】進位制.
【答案】A
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/5/27 14:0:0組卷:66引用:2難度:0.8
相似題
-
1.將389化成四進位制數的末位是( )
A.1 B.2 C.3 D.0 發布:2024/12/17 20:30:1組卷:124引用:22難度:0.9 -
2.將389化成四進位制數的末位是( )
A.1 B.2 C.3 D.0 發布:2024/12/17 20:30:1組卷:1引用:1難度:0.9 -
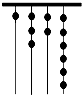 3.遠古時期,人們通過在繩子上打結來記錄數量,即“結繩計數”,如圖所示的是一位母親記錄的孩子自出生后的天數,在從右向左依次排列的不同繩子上打結,滿七進一,根據圖示可知,孩子已經出生的天數是( )
3.遠古時期,人們通過在繩子上打結來記錄數量,即“結繩計數”,如圖所示的是一位母親記錄的孩子自出生后的天數,在從右向左依次排列的不同繩子上打結,滿七進一,根據圖示可知,孩子已經出生的天數是( )A.336 B.510 C.1326 D.3603 發布:2024/10/26 17:0:2組卷:424引用:7難度:0.9


