請閱讀下列材料，并完成相應的任務．
梅涅勞斯（ Menelaus）是公元一世紀時的希臘數學家兼天文學家，著有幾何學和三角學方面的許多書籍．梅涅勞斯發現，三角形各邊（或其延長線）被一條不過任何一個頂點也不與任何一條邊平行的直線所截，這條直線可能與三角形的兩條邊相交（一定還會與一條邊的延長線相交），也可能與三條邊都不相交（與三條邊的延長線都相交）．他進行了深入研究并證明了著名的梅涅勞斯定理（簡稱梅氏定理）：
設D，E，F依次是△ABC的三邊AB，BC，CA或其延長線上的點，且這三點共線，則滿足ADDB?BEEC?CFFA=1．
這個定理的證明步驟如下：
情況①：如圖1，直線DE交△ABC的邊AB于點D，交邊AC于點F，交邊BC的延長線于點E．
過點C作CM∥DE交AB于點M，則BEEC=BDDM，ADDM=AFFC（依據）
∴BEEC?ADDM=BDDM?AFFC
∴BE?AD?FC=BD?AF?EC，即ADDB?BEEC?CFFA=1．
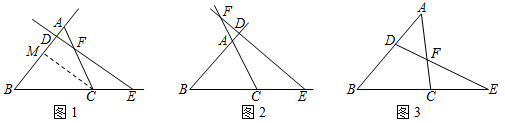
情況②：如圖2，直線DE分別交△ABC的邊BA，BC，CA的延長線于點D，E，F．
…
（1）情況①中的依據指：兩條直線被一組平行線所截，所得的對應線段成比例兩條直線被一組平行線所截，所得的對應線段成比例
（2）請你根據情況①的證明思路完成情況②的證明．
（3）如圖3，D，F分別是△ABC的邊AB，AC上的點，且AD：DB=CF：FA=2：3，連接DF并延長，交BC的延長線于點E，那么BE：CE=9494．
AD
DB
?
BE
EC
?
CF
FA
=
1
BE
EC
=
BD
DM
AD
DM
=
AF
FC
BE
EC
?
AD
DM
BD
DM
?
AF
FC
AD
DB
?
BE
EC
?
CF
FA
=
1
9
4
9
4
【考點】相似形綜合題．
【答案】兩條直線被一組平行線所截，所得的對應線段成比例；
9
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：819引用：3難度：0.1
相似題
-
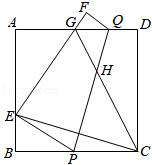1．如圖，將正方形紙片ABCD沿PQ折疊，使點C的對稱點E落在邊AB上，點D的對稱點為點F，EF交AD于點G，連接CG交PQ于點H，連接CE，EH．
（1）求證：△PBE∽△QFG；
（2）求∠ECG的度數；
（3）求證：EG2-CH2=GQ?GD．發布：2025/5/25 21:0:1組卷：400引用：2難度：0.3 -
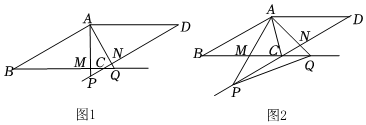2．如圖1，在菱形ABCD中，∠ABC是銳角，P、Q分別是邊DC、BC延長線上的動點，連接AP、AQ分別交BC、DC于點M、N．
（1）當AP⊥BC且∠PAQ=∠D時，證明：△ABM≌△ADN；
（2）如圖2，當∠PAQ=∠BCD時，連接AC、PQ．12
①證明：AC2=CP?CQ；
②若AB=4，AC=2，則當CM為何值時，△APQ是以PQ為底邊的等腰三角形．發布：2025/5/25 21:30:1組卷：184引用：1難度：0.1 -
3．【證明體驗】（1）如圖1，△ABC中，D為BC邊上任意一點，作DE⊥AC于E，若∠CDE=
∠A，求證：△ABC為等腰三角形；12
【嘗試應用】
（2）如圖2，四邊形ABCD中，∠D=90°，AD=CD，AE平分∠BAD，∠BCD+∠EAD=180°，若DE=2，AB=6，求AE的長；
【拓展延伸】
（3）如圖3，△ABC中，點D在AB邊上滿足CD=BD，∠ACB=90°+∠B，若AC=1012，BC=20，求AD的長．3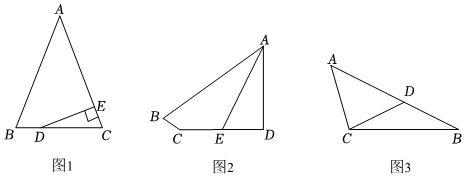
發布：2025/5/25 20:0:1組卷：497引用：1難度：0.3