當前位置：試卷中心 > 試卷詳情

2022年湖南省湘潭市湘潭縣錦石中學中考數學模擬試卷（一）

發布：2024/4/20 14:35:0

一、選擇題（本題有8個小題，每小題3分，共24分．）

1．在實數
1
3
、0、-1、-
2
中，最小的實數是（　　）
A．-
2
B．-1 C．0 D．
1
3
組卷：390引用：6難度：0.8
解析
2．下列計算正確的是（　　）
A．（x-1）²=x²-1 B．x⁸÷x²=x⁴
C．
2
+
3
=
5
D．（-x²y）³=-x⁶y³
組卷：140引用：3難度：0.7
解析
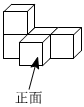3．如圖所示的幾何體的俯視圖是（　　）
A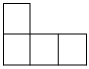． B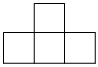． C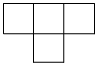． D．
組卷：15引用：2難度：0.8
解析
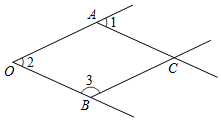4．如圖，是一個由4條線段構成的“魚”形圖案，其中OA∥BC，AC∥OB．若∠1=50°，則∠3的度數為（　　）
A．130° B．120° C．50° D．125°
組卷：782引用：10難度：0.6
解析
5．已知關于x的一元二次方程（k+1）x²+2x-1=0有實數根，則k的取值范圍是（　　）
A．k≥-2 B．k≥-2且k≠-1 C．k≥2 D．k≤-2
組卷：1618引用：9難度：0.7
解析
6．國家隊要從甲、乙、丙、丁四名隊員中選出一名隊員參加2022年北京冬奧會1000米速度滑冰比賽，對這四名隊員進行了10次速度測試，經過數據分析4人的平均成績均為95分，S_甲²=0.028，S_乙²=0.06，S_丙²=0.015，S_丁²=0.32．則應該選擇（　　）
A．甲 B．乙 C．丙 D．丁
組卷：11引用：1難度：0.7
解析
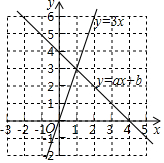7．數形結合是數學解題中常用的思想方法，使用數形結合的方法，很多問題可迎刃而解，且解法簡潔．如圖，直線y=3x和直線y=ax+b交于點（1，3），根據圖象分析，方程3x=ax+b的解為（　　）
A．x=1 B．x=-1 C．x=3 D．x=-3
組卷：1759引用：12難度：0.8
解析
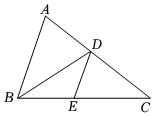8．如圖，△ABC中，BD是∠ABC的平分線，DE∥AB交BC于E，EC=6，BE=4，則AB長為（　　）
A．6 B．8 C．
20
3
D．
24
5
組卷：557引用：10難度：0.4
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本題有10個小題，共72分．）

25．請閱讀下列材料，并完成相應的任務．
梅涅勞斯（ Menelaus）是公元一世紀時的希臘數學家兼天文學家，著有幾何學和三角學方面的許多書籍．梅涅勞斯發現，三角形各邊（或其延長線）被一條不過任何一個頂點也不與任何一條邊平行的直線所截，這條直線可能與三角形的兩條邊相交（一定還會與一條邊的延長線相交），也可能與三條邊都不相交（與三條邊的延長線都相交）．他進行了深入研究并證明了著名的梅涅勞斯定理（簡稱梅氏定理）：
設D，E，F依次是△ABC的三邊AB，BC，CA或其延長線上的點，且這三點共線，則滿足
AD
DB
?
BE
EC
?
CF
FA
=
1
．
這個定理的證明步驟如下：
情況①：如圖1，直線DE交△ABC的邊AB于點D，交邊AC于點F，交邊BC的延長線于點E．
過點C作CM∥DE交AB于點M，則
BE
EC
=
BD
DM
，
AD
DM
=
AF
FC
（依據）
∴
BE
EC
?
AD
DM
=
BD
DM
?
AF
FC

∴BE?AD?FC=BD?AF?EC，即
AD
DB
?
BE
EC
?
CF
FA
=
1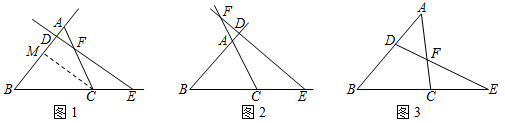
．

情況②：如圖2，直線DE分別交△ABC的邊BA，BC，CA的延長線于點D，E，F．
…
（1）情況①中的依據指：

（2）請你根據情況①的證明思路完成情況②的證明．
（3）如圖3，D，F分別是△ABC的邊AB，AC上的點，且AD：DB=CF：FA=2：3，連接DF并延長，交BC的延長線于點E，那么BE：CE=
．
組卷：819引用：3難度：0.1
解析
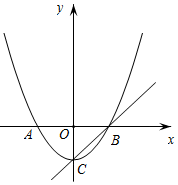26．如圖，已知頂點為C（0，-3）的拋物線y=ax²+b（a≠0）與x軸交于A，B兩點，直線y=x+m過頂點C和點B．
（1）求m的值；
（2）求函數y=ax²+b（a≠0）的解析式；
（3）拋物線上是否存在點M，使得∠MCB=15°？若存在，求出點M的坐標；若不存在，請說明理由．
組卷：5854引用：13難度：0.3
解析