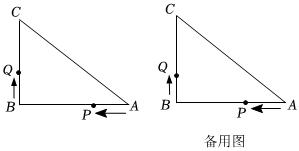
如圖，已知△ABC中，∠B=90°，AB=8cm,BC=6cm,P、Q是△ABC邊上的兩個動點，其中點P從點A開始沿A→B方向運動，且速度為每秒1cm,點Q從點B開始沿B→C→A方向運動，且速度為每秒2cm,它們同時出發，設出發的時間為t秒．
（1）出發1秒后，求PQ的長；
（2）若點Q運動到邊AC上，求能使△BCQ成為直角三角形的運動時間；
（3）若點Q運動到邊AC上，求能使△BCQ成為等腰三角形的運動時間．
【考點】三角形綜合題．
【答案】（1）cm；
（2）若點Q運動到邊AC上，能使△BCQ成為直角三角形的運動時間為4.8秒或8秒；
（3）若點Q運動到邊AC上，能使△BCQ成為等腰三角形的運動時間為6.6秒或6秒或5.5秒．
53
（2）若點Q運動到邊AC上，能使△BCQ成為直角三角形的運動時間為4.8秒或8秒；
（3）若點Q運動到邊AC上，能使△BCQ成為等腰三角形的運動時間為6.6秒或6秒或5.5秒．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/13 13:0:8組卷：89引用：1難度：0.5
相似題
-
1．如圖1，△ABC和△CDE都是等邊三角形，且A，C，E在同一條直線上，分別連接AD，BE．
（1）求證：AD=BE；
（2）如圖2，連接BD，若M，N，Q分別為AB，DE，BD的中點，過N作NP⊥MN與MQ的延長線交于P，求證：MP=AD；
（3）如圖3，設AD與BE交于F點，點M在AB上，MG∥AD，交BE于H，交CF的延長線于G，試判斷△FGH的形狀．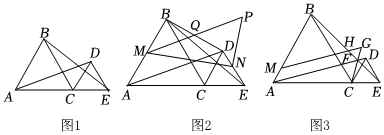
發布：2025/5/24 17:0:2組卷：45引用：1難度：0.1 -
2．如圖，在△ABC中，∠A=α（0°＜α≤90°），將BC邊繞點C逆時針旋轉（180°-α）得到線段CD．
（1）判斷∠B與∠ACD的數量關系并證明；
（2）將AC邊繞點C順時針旋轉α得到線段CE，連接DE與AC邊交于點M（不與點A，C重合）．
①用等式表示線段DM，EM之間的數量關系，并證明；
②若AB=a,AC=b,直接寫出AM的長．（用含a,b的式子表示）發布：2025/5/24 14:0:2組卷：1301引用：9難度：0.2 -
3．（1）如圖1，Rt△ABC中，∠C=90°，AB=10，AC=8，E是AC上一點，AE=5，ED⊥AB，垂足為D，求AD的長．
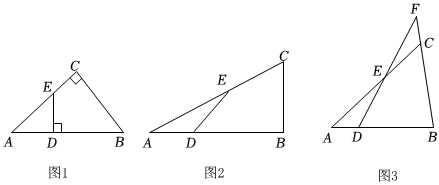
（2）類比探究：如圖2，△ABC中，AC=14，BC=6，點D，E分別在線段AB，AC上，∠EDB=∠ACB=60°，DE=2．求AD的長．
（3）拓展延伸：如圖3，△ABC中，點D，點E分別在線段AB，AC上，∠EDB=∠ACB=60°．延長DE，BC交于點F，AD=4，DE=5，EF=6，DE＜BD，=；BD=．BCAC發布：2025/5/24 16:30:1組卷：1046引用：6難度：0.1